المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Beurling,s Function |
 1280
 04:01 مساءً
date: 7-8-2019 |
Author : Beurling, A. 
Book or Source : "Sur les intégrales de Fourier absolument convergentes et leur application à fonctionelle." Neuvième congrès des mathématiciens scandinaves.... 
Page and Part : ...|
Read More
Date:
1804
Date: 10-5-2018
2106
Date: 16-8-2018
3793
|
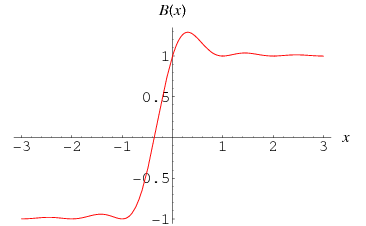
The entire function
 |
 |
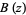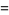![[(sin(piz))/pi]^2[2/z+sum_(n=0)^(infty)1/((z-n)^2)-sum_(n=1)^(infty)1/((z+n)^2)]](http://mathworld.wolfram.com/images/equations/BeurlingsFunction/Inline3.gif) |
(1) |
 |
 |
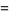![1-(2sin^2(piz))/(pi^2z^2)[z^2psi_1(z)-z-1],](http://mathworld.wolfram.com/images/equations/BeurlingsFunction/Inline6.gif) |
(2) |
where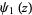 
is a polygamma function.
It satisfies ![B(z)=O(e^(2pi(I[z])))](http://mathworld.wolfram.com/images/equations/BeurlingsFunction/Inline8.gif)
and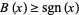 
for all real 
. Amazingly, it also has the integral
![int_(-infty)^infty[B(x)-sgn(x)]dx=1.](http://mathworld.wolfram.com/images/equations/BeurlingsFunction/NumberedEquation1.gif) |
(3) |
Furthermore, among all functions with the first two properties,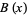 
minimizes the integral (3) (Beurling 1938, Montgomery 2001).
REFERENCES:
Beurling, A. "Sur les intégrales de Fourier absolument convergentes et leur application à fonctionelle." Neuvième congrès des mathématiciens scandinaves. Helsingfors, 1938.
Montgomery, H. L. "Harmonic Analysis as Found in Analytic Number Theory." In Twentieth Century Harmonic Analysis--A Celebration. Proceedings of the NATO Advanced Study Institute Held in Il Ciocco, July 2-15, 2000 (Ed. J. S. Byrnes). Dordrecht, Netherlands: Kluwer, pp. 271-293, 2001.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|
