


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-8-2019
Date: 22-4-2019
Date: 25-9-2019
|
Orthogonal polynomials are classes of polynomials 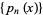 defined over a range
defined over a range ![[a,b]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline2.gif) that obey an orthogonalityrelation
that obey an orthogonalityrelation
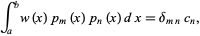 |
(1)
|
where 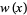 is a weighting function and
is a weighting function and 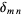 is the Kronecker delta. If
is the Kronecker delta. If 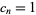 , then the polynomials are not only orthogonal, but orthonormal.
, then the polynomials are not only orthogonal, but orthonormal.
Orthogonal polynomials have very useful properties in the solution of mathematical and physical problems. Just as Fourier series provide a convenient method of expanding a periodic function in a series of linearly independent terms, orthogonal polynomials provide a natural way to solve, expand, and interpret solutions to many types of important differential equations. Orthogonal polynomials are especially easy to generate using Gram-Schmidt orthonormalization.
A table of common orthogonal polynomials is given below, where 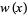 is the weighting function and
is the weighting function and
![c_n=int_a^bw(x)[p_n(x)]^2dx](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/NumberedEquation2.gif) |
(2)
|
(Abramowitz and Stegun 1972, pp. 774-775).
| polynomial | interval | 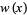 |
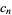 |
| Chebyshev polynomial of the first kind | ![[-1,1]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline9.gif) |
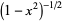 |
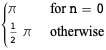 |
| Chebyshev polynomial of the second kind | ![[-1,1]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline12.gif) |
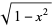 |
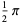 |
| Gegenbauer polynomial | ![[-1,1]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline15.gif) |
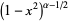 |
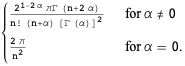 |
| Hermite polynomial |  |
 |
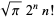 |
| Jacobi polynomial | 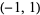 |
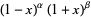 |
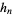 |
| Laguerre polynomial | 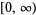 |
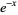 |
1 |
| generalized Laguerre polynomial | 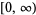 |
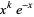 |
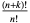 |
| Legendre polynomial | ![[-1,1]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline29.gif) |
1 | 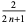 |
In the above table,
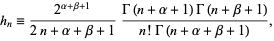 |
(3)
|
where 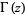 is a gamma function.
is a gamma function.
The roots of orthogonal polynomials possess many rather surprising and useful properties. For instance, let 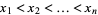 be the roots of the
be the roots of the 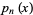 with
with 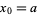 and
and 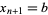 . Then each interval
. Then each interval ![[x_nu,x_(nu+1)]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline36.gif) for
for 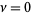 , 1, ...,
, 1, ..., 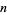 contains exactly one root of
contains exactly one root of 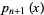 . Between two roots of
. Between two roots of 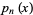 there is at least one root of
there is at least one root of 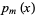 for
for 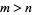 .
.
Let 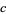 be an arbitrary real constant, then the polynomial
be an arbitrary real constant, then the polynomial
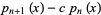 |
(4)
|
has 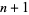 distinct real roots. If
distinct real roots. If 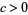 (
(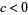 ), these roots lie in the interior of
), these roots lie in the interior of ![[a,b]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline47.gif) , with the exception of the greatest (least) root which lies in
, with the exception of the greatest (least) root which lies in ![[a,b]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline48.gif) only for
only for
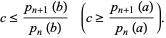 |
(5)
|
The following decomposition into partial fractions holds
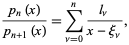 |
(6)
|
where 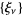 are the roots of
are the roots of 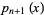 and
and
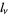 |
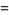 |
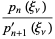 |
(7)
|
 |
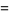 |
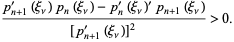 |
(8)
|
Another interesting property is obtained by letting 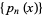 be the orthonormal set of polynomials associated with the distribution
be the orthonormal set of polynomials associated with the distribution 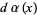 on
on ![[a,b]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline59.gif) . Then the convergents
. Then the convergents 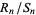 of the continued fraction
of the continued fraction
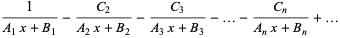 |
(9)
|
are given by
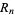 |
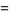 |
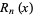 |
(10)
|
 |
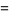 |
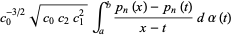 |
(11)
|
 |
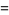 |
 |
(12)
|
where 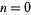 , 1, ... and
, 1, ... and
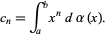 |
(13)
|
Furthermore, the roots of the orthogonal polynomials 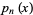 associated with the distribution
associated with the distribution 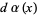 on the interval
on the interval ![[a,b]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline73.gif) are real and distinct and are located in the interior of the interval
are real and distinct and are located in the interior of the interval ![[a,b]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline74.gif) .
.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Orthogonal Polynomials." Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 771-802, 1972.
Arfken, G. "Orthogonal Polynomials." Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 520-521, 1985.
Chihara, T. S. An Introduction to Orthogonal Polynomials. New York: Gordon and Breach, 1978.
Gautschi, W.; Golub, G. H.; and Opfer, G. (Eds.) Applications and Computation of Orthogonal Polynomials, Conference at the Mathematical Research Institute Oberwolfach, Germany, March 22-28, 1998. Basel, Switzerland: Birkhäuser, 1999.
Iyanaga, S. and Kawada, Y. (Eds.). "Systems of Orthogonal Functions." Appendix A, Table 20 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1477, 1980.
Koekoek, R. and Swarttouw, R. F. The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 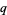 -Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, 1-168, 1998.
-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, 1-168, 1998.
Nikiforov, A. F.; Uvarov, V. B.; and Suslov, S. S. Classical Orthogonal Polynomials of a Discrete Variable. New York: Springer-Verlag, 1992.
Sansone, G. Orthogonal Functions. New York: Dover, 1991.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 44-47 and 54-55, 1975.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|