


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-4-2019
Date: 12-10-2018
Date: 3-6-2019
|
A hypergeometric series 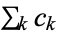 is a series for which
is a series for which 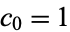 and the ratio of consecutive terms is a rational function of the summation index
and the ratio of consecutive terms is a rational function of the summation index 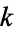 , i.e., one for which
, i.e., one for which
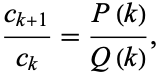 |
(1) |
with 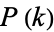 and
and 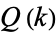 polynomials. In this case,
polynomials. In this case, 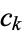 is called a hypergeometric term (Koepf 1998, p. 12). The functions generated by hypergeometric series are called hypergeometric functions or, more generally, generalized hypergeometric functions. If the polynomials are completely factored, the ratio of successive terms can be written
is called a hypergeometric term (Koepf 1998, p. 12). The functions generated by hypergeometric series are called hypergeometric functions or, more generally, generalized hypergeometric functions. If the polynomials are completely factored, the ratio of successive terms can be written
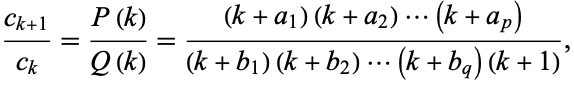 |
(2) |
where the factor of 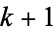 in the denominator is present for historical reasons of notation, and the resulting generalized hypergeometric function is written
in the denominator is present for historical reasons of notation, and the resulting generalized hypergeometric function is written
![_pF_q[a_1 a_2 ... a_p; b_1 b_2 ... b_q;x]=sum_(k=0)c_kx^k.](http://mathworld.wolfram.com/images/equations/HypergeometricSeries/NumberedEquation3.gif) |
(3) |
If 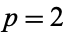 and
and 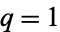 , the function becomes a traditional hypergeometric function
, the function becomes a traditional hypergeometric function 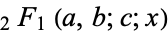 .
.
Many sums can be written as generalized hypergeometric functions by inspections of the ratios of consecutive terms in the generating hypergeometric series.
REFERENCES:
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, 1998.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. "Hypergeometric Series," "How to Identify a Series as Hypergeometric," and "Software That Identifies Hypergeometric Series." §3.2-3.4 in A=B. Wellesley, MA: A K Peters, pp. 34-42, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|