


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-9-2018
Date: 30-3-2019
Date: 2-5-2019
|
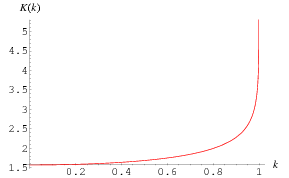
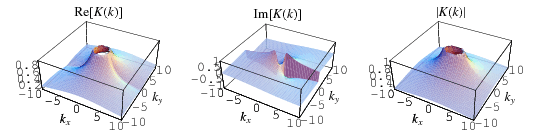
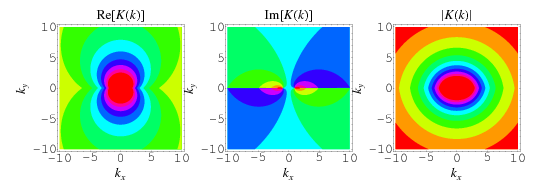
The complete elliptic integral of the first kind 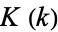 , illustrated above as a function of the elliptic modulus
, illustrated above as a function of the elliptic modulus 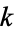 , is defined by
, is defined by
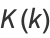 |
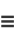 |
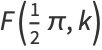 |
(1) |
 |
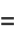 |
![pi/2sum_(n=0)^(infty)[((2n-1)!!)/((2n)!!)]^2k^(2n)](http://mathworld.wolfram.com/images/equations/CompleteEllipticIntegraloftheFirstKind/Inline8.gif) |
(2) |
 |
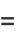 |
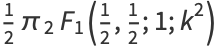 |
(3) |
where 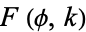 is the incomplete elliptic integral of the first kind and
is the incomplete elliptic integral of the first kind and 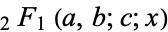 is the hypergeometric function.
is the hypergeometric function.
It is implemented in the Wolfram Language as EllipticK[m], where 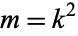 is the parameter.
is the parameter.
It satisfies the identity
 |
(4) |
where 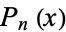 is a Legendre polynomial. This simplifies to
is a Legendre polynomial. This simplifies to
 |
(5) |
for all complex values of 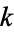 except possibly for real
except possibly for real 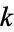 with
with 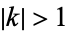 .
.
In addition, 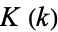 satisfies the identity
satisfies the identity
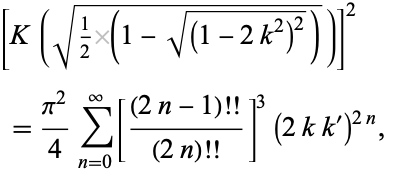 |
(6) |
where 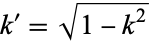 is the complementary modulus. Amazingly, this reduces to the beautiful form
is the complementary modulus. Amazingly, this reduces to the beautiful form
 |
(7) |
for 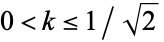 (Watson 1908, 1939).
(Watson 1908, 1939).
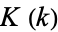 can be computed in closed form for special values of
can be computed in closed form for special values of 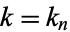 , where
, where 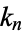 is a called an elliptic integral singular value. Other special values include
is a called an elliptic integral singular value. Other special values include
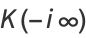 |
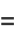 |
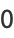 |
(8) |
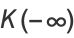 |
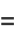 |
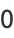 |
(9) |
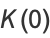 |
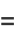 |
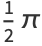 |
(10) |
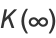 |
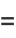 |
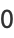 |
(11) |
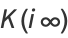 |
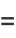 |
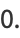 |
(12) |
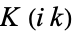 satisfies
satisfies
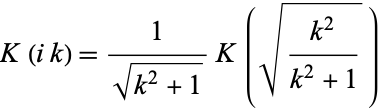 |
(13) |
possibly modulo issues of 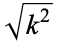 , which can be derived from equation 17.4.17 in Abramowitz and Stegun (1972, p. 593).
, which can be derived from equation 17.4.17 in Abramowitz and Stegun (1972, p. 593).
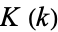 is related to the Jacobi elliptic functions through
is related to the Jacobi elliptic functions through
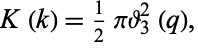 |
(14) |
where the nome is defined by
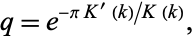 |
(15) |
with 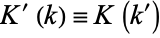 , where
, where 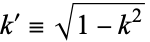 is the complementary modulus.
is the complementary modulus.
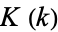 satisfies the Legendre relation
satisfies the Legendre relation
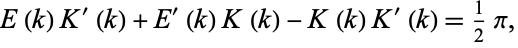 |
(16) |
where 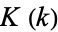 and
and 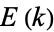 are complete elliptic integrals of the first and second kinds, respectively, and
are complete elliptic integrals of the first and second kinds, respectively, and 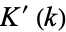 and
and 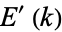 are the complementary integrals. The modulus
are the complementary integrals. The modulus 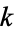 is often suppressed for conciseness, so that
is often suppressed for conciseness, so that 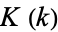 and
and 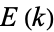 are often simply written
are often simply written 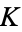 and
and 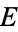 , respectively.
, respectively.
The integral 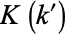 for complementary modulus is given by
for complementary modulus is given by
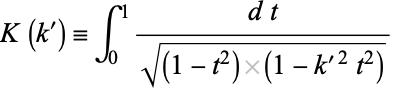 |
(17) |
(Whittaker and Watson 1990, p. 501), and
 |
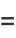 |
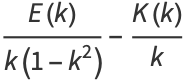 |
(18) |
 |
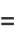 |
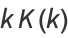 |
(19) |
(Whittaker and Watson 1990, p. 521), so
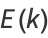 |
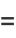 |
![k(1-k^2)[(dK)/(dk)+(K(k))/k]](http://mathworld.wolfram.com/images/equations/CompleteEllipticIntegraloftheFirstKind/Inline64.gif) |
(20) |
 |
 |
![(1-k^2)[k(dK)/(dk)+K(k)]](http://mathworld.wolfram.com/images/equations/CompleteEllipticIntegraloftheFirstKind/Inline67.gif) |
(21) |
(cf. Whittaker and Watson 1990, p. 521).
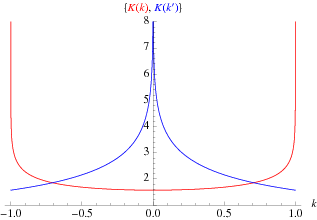
The solution to the differential equation
![d/(dk)[k(1-k^2)(dy)/(dk)]-ky=0](http://mathworld.wolfram.com/images/equations/CompleteEllipticIntegraloftheFirstKind/NumberedEquation10.gif) |
(22) |
(Zwillinger 1997, p. 122; Gradshteyn and Ryzhik 2000, p. 907) is
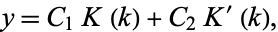 |
(23) |
where the two solutions are illustrated above and 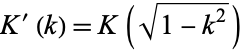 .
.
Definite integrals of 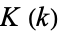 include
include
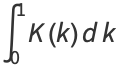 |
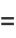 |
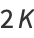 |
(24) |
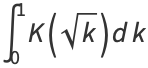 |
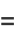 |
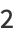 |
(25) |
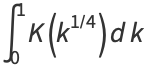 |
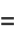 |
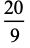 |
(26) |
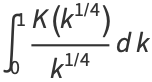 |
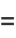 |
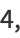 |
(27) |
where 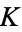 (not to be confused with
(not to be confused with 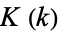 ) is Catalan's constant.
) is Catalan's constant.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
Watson G. N. "The Expansion of Products of Hypergeometric Functions." Quart. J. Pure Appl. Math. 39, 27-51, 1907.
Watson G. N. "A Series for the Square of the Hypergeometric Function." Quart. J. Pure Appl. Math. 40, 46-57, 1908.
Watson, G. N. "Three Triple Integrals." Quart. J. Math., Oxford Ser. 2 10, 266-276, 1939.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 122, 1997.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
المجمع العلمي يقيم ورشة تطويرية ودورة قرآنية في النجف والديوانية
|
|
|