


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-8-2019
Date: 18-8-2018
Date: 24-9-2019
|
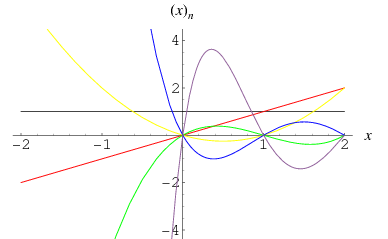
The falling factorial 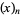 , sometimes also denoted
, sometimes also denoted  (Graham et al. 1994, p. 48), is defined by
(Graham et al. 1994, p. 48), is defined by
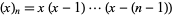 |
(1) |
for 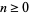 . Is also known as the binomial polynomial, lower factorial, falling factorial power (Graham et al. 1994, p. 48), or factorial power.
. Is also known as the binomial polynomial, lower factorial, falling factorial power (Graham et al. 1994, p. 48), or factorial power.
The falling factorial is related to the rising factorial 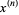 (a.k.a. Pochhammer symbol) by
(a.k.a. Pochhammer symbol) by
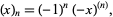 |
(2) |
The falling factorial is implemented in the Wolfram Language as FactorialPower[x, n].
A generalized version of the falling factorial can defined by
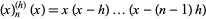 |
(3) |
and is implemented in the Wolfram Language as FactorialPower[x, n, h].
The usual factorial is related to the falling factorial by
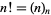 |
(4) |
(Graham et al. 1994, p. 48).
In combinatorial usage, the falling factorial is commonly denoted 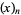 and the rising factorial is denoted
and the rising factorial is denoted 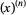 (Comtet 1974, p. 6; Roman 1984, p. 5; Hardy 1999, p. 101), whereas in the calculus of finite differences and the theory of special functions, the falling factorial is denoted
(Comtet 1974, p. 6; Roman 1984, p. 5; Hardy 1999, p. 101), whereas in the calculus of finite differences and the theory of special functions, the falling factorial is denoted 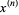 and the rising factorial is denoted
and the rising factorial is denoted 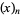 (Roman 1984, p. 5; Abramowitz and Stegun 1972, p. 256; Spanier 1987). Extreme caution is therefore needed in interpreting the meanings of the notations
(Roman 1984, p. 5; Abramowitz and Stegun 1972, p. 256; Spanier 1987). Extreme caution is therefore needed in interpreting the meanings of the notations 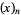 and
and 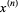 . In this work, the notation
. In this work, the notation 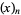 is used for the falling factorial, potentially causing confusion with the Pochhammer symbol.
is used for the falling factorial, potentially causing confusion with the Pochhammer symbol.
The first few falling factorials are
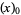 |
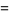 |
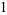 |
(5) |
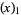 |
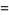 |
 |
(6) |
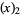 |
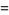 |
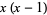 |
(7) |
 |
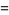 |
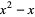 |
(8) |
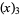 |
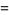 |
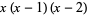 |
(9) |
 |
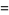 |
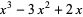 |
(10) |
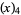 |
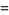 |
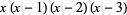 |
(11) |
 |
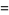 |
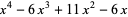 |
(12) |
(OEIS A054654).
The derivative is given by
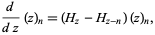 |
(13) |
where 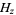 is a harmonic number.
is a harmonic number.
A sum formula connecting the falling factorial 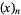 and rising factorial
and rising factorial 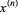 ,
,
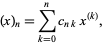 |
(14) |
is given using the Sheffer formalism with
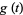 |
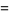 |
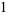 |
(15) |
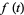 |
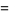 |
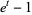 |
(16) |
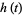 |
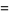 |
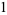 |
(17) |
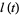 |
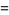 |
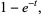 |
(18) |
which gives the generating function
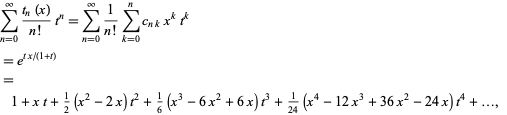 |
(19) |
where
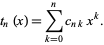 |
(20) |
Reading the coefficients off gives
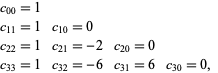 |
(21) |
so,
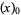 |
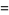 |
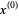 |
(22) |
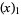 |
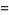 |
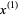 |
(23) |
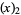 |
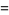 |
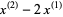 |
(24) |
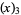 |
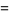 |
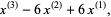 |
(25) |
etc. (and the formula given by Roman 1984, p. 133, is incorrect).
The falling factorial is an associated Sheffer sequence with
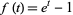 |
(26) |
(Roman 1984, p. 29), and has generating function
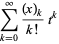 |
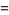 |
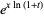 |
(27) |
 |
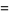 |
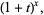 |
(28) |
which is equivalent to the binomial theorem
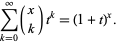 |
(29) |
The binomial identity of the Sheffer sequence is
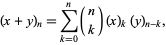 |
(30) |
where 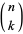 is a binomial coefficient, which can be rewritten as
is a binomial coefficient, which can be rewritten as
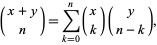 |
(31) |
known as the Chu-Vandermonde identity. The falling factorials obey the recurrence relation
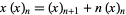 |
(32) |
(Roman 1984, p. 61).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.
Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, 1974.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 101, 1999.
Roman, S. "The Lower Factorial Polynomial." §1.2 in The Umbral Calculus. New York: Academic Press, pp. 5, 28-29, and 56-63, 1984.
Sloane, N. J. A. Sequences A054654 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Pochhammer Polynomials 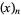 ." Ch. 18 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 149-165, 1987.
." Ch. 18 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 149-165, 1987.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|