


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-8-2018
Date: 25-7-2019
Date: 13-9-2019
|
The Gaussian integral, also called the probability integral and closely related to the erf function, is the integral of the one-dimensional Gaussian function over 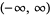 . It can be computed using the trick of combining two one-dimensional Gaussians
. It can be computed using the trick of combining two one-dimensional Gaussians
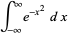 |
 |
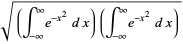 |
(1) |
 |
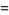 |
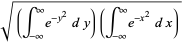 |
(2) |
 |
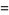 |
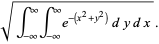 |
(3) |
Here, use has been made of the fact that the variable in the integral is a dummy variable that is integrates out in the end and hence can be renamed from  to
to 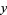 . Switching to polar coordinates then gives
. Switching to polar coordinates then gives
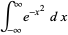 |
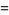 |
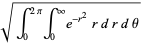 |
(4) |
 |
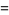 |
![sqrt(2pi[-1/2e^(-r^2)]_0^infty)](http://mathworld.wolfram.com/images/equations/GaussianIntegral/Inline18.gif) |
(5) |
 |
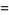 |
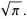 |
(6) |
There also exists a simple proof of this identity that does not require transformation to polar coordinates (Nicholas and Yates 1950).
The integral from 0 to a finite upper limit 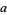 can be given by the continued fraction
can be given by the continued fraction
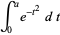 |
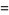 |
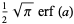 |
(7) |
 |
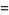 |
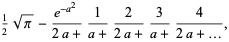 |
(8) |
where 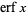 is erf (the error function), as first stated by Laplace, proved by Jacobi, and rediscovered by Ramanujan (Watson 1928; Hardy 1999, pp. 8-9).
is erf (the error function), as first stated by Laplace, proved by Jacobi, and rediscovered by Ramanujan (Watson 1928; Hardy 1999, pp. 8-9).
The general class of integrals of the form
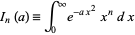 |
(9) |
can be solved analytically by setting
 |
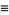 |
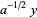 |
(10) |
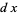 |
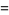 |
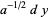 |
(11) |
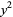 |
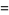 |
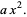 |
(12) |
Then
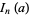 |
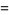 |
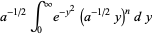 |
(13) |
 |
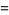 |
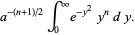 |
(14) |
For 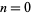 , this is just the usual Gaussian integral, so
, this is just the usual Gaussian integral, so
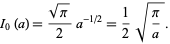 |
(15) |
For 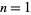 , the integrand is integrable by quadrature,
, the integrand is integrable by quadrature,
![I_1(a)=a^(-1)int_0^inftye^(-y^2)ydy=a^(-1)[-1/2e^(-y^2)]_0^infty=1/2a^(-1).](http://mathworld.wolfram.com/images/equations/GaussianIntegral/NumberedEquation3.gif) |
(16) |
To compute 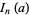 for
for 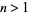 , use the identity
, use the identity
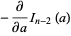 |
 |
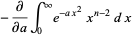 |
(17) |
 |
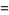 |
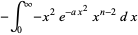 |
(18) |
 |
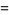 |
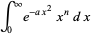 |
(19) |
 |
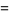 |
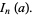 |
(20) |
For 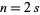 even,
even,
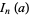 |
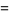 |
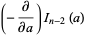 |
(21) |
 |
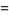 |
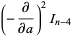 |
(22) |
 |
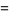 |
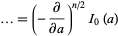 |
(23) |
 |
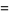 |
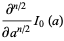 |
(24) |
 |
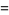 |
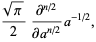 |
(25) |
so
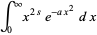 |
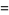 |
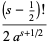 |
(26) |
 |
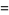 |
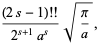 |
(27) |
where 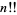 is a double factorial. If
is a double factorial. If 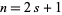 is odd, then
is odd, then
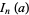 |
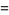 |
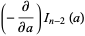 |
(28) |
 |
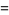 |
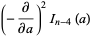 |
(29) |
 |
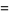 |
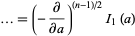 |
(30) |
 |
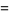 |
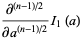 |
(31) |
 |
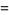 |
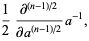 |
(32) |
so
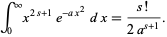 |
(33) |
The solution is therefore
![int_0^inftye^(-ax^2)x^ndx={((n-1)!!)/(2^(n/2+1)a^(n/2))sqrt(pi/a) for n even; ([1/2(n-1)]!)/(2a^((n+1)/2)) for n odd.](http://mathworld.wolfram.com/images/equations/GaussianIntegral/NumberedEquation5.gif) |
(34) |
The first few values are therefore
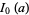 |
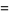 |
 |
(35) |
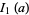 |
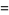 |
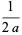 |
(36) |
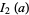 |
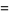 |
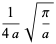 |
(37) |
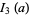 |
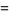 |
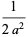 |
(38) |
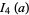 |
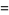 |
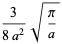 |
(39) |
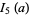 |
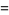 |
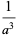 |
(40) |
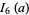 |
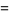 |
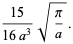 |
(41) |
A related, often useful integral is
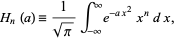 |
(42) |
which is simply given by
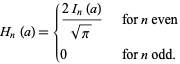 |
(43) |
The more general integral of 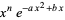 has the following closed forms,
has the following closed forms,
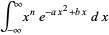 |
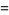 |
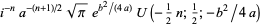 |
(44) |
 |
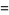 |
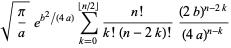 |
(45) |
 |
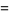 |
 |
(46) |
for integer  (F. Pilolli, pers. comm.). For (45) and (46),
(F. Pilolli, pers. comm.). For (45) and (46), 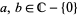 (the punctured plane),
(the punctured plane), ![R[a]>0](http://mathworld.wolfram.com/images/equations/GaussianIntegral/Inline133.gif) , and
, and 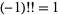 . Here,
. Here, 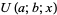 is a confluent hypergeometric function of the second kind and
is a confluent hypergeometric function of the second kind and 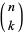 is a binomial coefficient.
is a binomial coefficient.
REFERENCES:
Guitton, E. "Démonstration de la formule." Nouv. Ann. Math. 65, 237-239, 1906.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Nicholas, C. B. and Yates, R. C. "The Probability Integral." Amer. Math. Monthly 57, 412-413, 1950.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 147-148, 1984.
Watson, G. N. "Theorems Stated by Ramanujan (IV): Theorems on Approximate Integration and Summation of Series." J. London Math. Soc. 3, 282-289, 1928.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
جامعة الفلوجة: حفل تخرج طلبة الجامعات يهدف إلى جمع الطلبة تحت خيمة العراق الموحد
|
|
|