
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-9-2019
Date: 29-6-2019
Date: 14-5-2018
|
Let 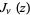 be a Bessel function of the first kind,
be a Bessel function of the first kind, 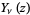 a Bessel function of the second kind, and
a Bessel function of the second kind, and 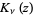 a modified Bessel function of the first kind. Also let
a modified Bessel function of the first kind. Also let ![R[z]>0](http://mathworld.wolfram.com/images/equations/WatsonsFormula/Inline4.gif) and require
and require ![R[mu-nu]<1](http://mathworld.wolfram.com/images/equations/WatsonsFormula/Inline5.gif) . Then
. Then
![J_mu(z)Y_nu(z)-J_nu(z)Y_mu(z)=(4sin[(mu-nu)pi])/(pi^2)int_0^inftyK_(nu-mu)(2zsinht)e^(-(mu+nu)t)dt.](http://mathworld.wolfram.com/images/equations/WatsonsFormula/NumberedEquation1.gif) |
The fourth edition of Gradshteyn and Ryzhik (2000), Iyanaga and Kawada (1980), and Ito (1987) erroneously give the exponential with a plus sign. A related integral is given by
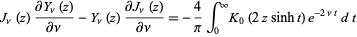 |
for ![R[z]>0](http://mathworld.wolfram.com/images/equations/WatsonsFormula/Inline6.gif) .
.
REFERENCES:
Gradshteyn, I. S. and Ryzhik, I. M. Eqns. 6.617.1 and 6.617.2 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. 710, 2000.
Itô, K. (Ed.). Encyclopedic Dictionary of Mathematics, 2nd ed. Cambridge, MA: MIT Press, p. 1806, 1987.
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1476, 1980.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|