Tetrahedral Equation

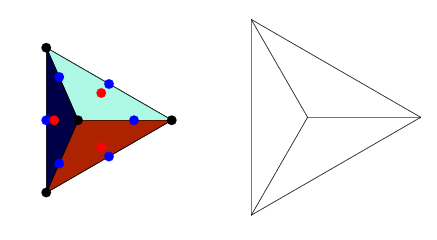
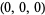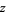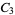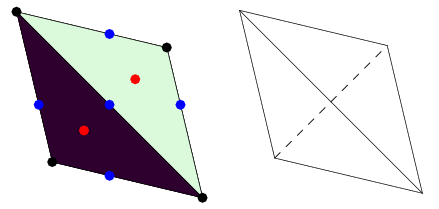
The tetrahedral equation, by way of analogy with the icosahedral equation, is a set of related equations derived from the projective geometry of the octahedron. Consider a tetrahedron centered , oriented with -axis along a fourfold () rotational symmetry axis, and with one of the top three edges lying in the 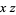-plane (left figure). In this figure, vertices are shown in black, face centers in red, and edge midpoints in blue.

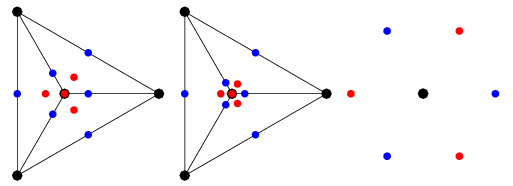
The simplest tetrahedral equation is defined by projecting the vertices of the tetrahedron with unit circumradius using a stereographic projection from the south pole of its circumsphere onto the plane 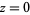, and expressing these vertex locations (interpreted as complex quantities in the complex 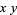-plane) as roots of an algebraic equation. The resulting projection is shown as the left figure above, with black dots being the vertex positions. The resulting equation is

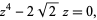(1)

where 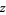 here refers to the coordinate in the complex plane (not the height above the projection plane).

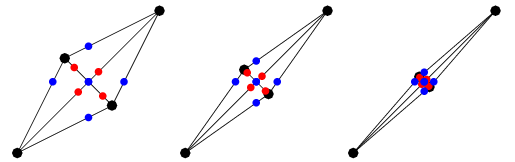
If the tetrahedron with unit inradius is instead projected (second figure above), the equation expressing the positions of the face centers (red dots) is given by

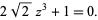(2)

Finally, if the octahedron with unit midradius is projected (right figure above), the equation expressing the positions of the edge midpoints (blue dots) is given by

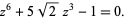(3)

Note that because these equations involve variables to multiples of the power 3, rotating the solid by 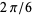 radians changes transforms the quantities from  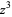to 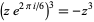, producing the same equations modulo minus signs in odd powers of 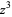, corresponding to flipping the positions of the roots about the imaginary axis.

If the tetrahedron is instead oriented so that the top and bottom faces are parallel to the 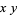-plane, the corresponding equations giving projected vertices, face centers, and edge midpoints are

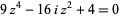	(4)
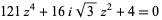	(5)
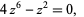	(6)

respectively.