


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-3-2017
Date: 11-3-2019
Date: 19-1-2019
|
What is a "root"?
A root is a value for which a given function equals zero. When that function is plotted on a graph, the roots are points where the function crosses the x-axis.
For a function, f(x), the roots are the values of x for which f(x)=0. For example, with the function f(x)=2-x, the only root would be x = 2, because that value produces f(x)=0.
Of course, it's easy to find the roots of a trivial problem like that one, but what about something crazy like this:
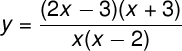
Steps to find roots of rational functions
Numerator Factors
Remember that a factor is something being multiplied or divided, such as (2x-3) in the above example. So, the two factors in the numerator are (2x-3) and (x+3). If either of those factors can be zero, then the whole function will be zero. It won't matter (well, there is an exception) what the rest of the function says, because you're multiplying by a term that equals zero.
So, the point is, figure out how to make the numerator zero and you've found your roots (also known as zeros, for obvious reasons!). In this example, we have two factors in the numerator, so either one can be zero. Let's set them both equal to zero and then solve for the x values:
2x - 3 = 0
2x = 3
x = 3/2
AND
x + 3 = 0
x = -3
So, x = 3/2 and x = -3 become our roots for this function. They're also the x-intercepts when plotted on a graph, because y will equal 0 when x is 3/2 or -3.
Denominator Factors
Just like with the numerator, there are two factors being multiplied in the denominators. They are x and x-2. Let's set them both equal to zero and solve them:
x = 0
AND
x - 2 = 0
x = 2
Those are not roots of this function. Look what happens when we plug in either 0 or 2 for x. We get a zero in the denominator, which means division by zero. That means the function does not exist at this point. In fact, x = 0 and x = 2 become our vertical asymptotes (zeros of the denominator). So, there is a vertical asymptote at x = 0 and x = 2 for the above function.
Here's a geometric view of what the above function looks like including BOTH x-intercepts and BOTH vertical asymptotes:
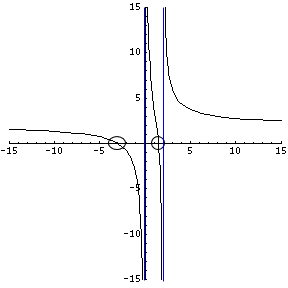
Summary
Roots of a function are x-values for which the function equals zero. They are also known as zeros.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|