Wiener-Hopf Method

The Wiener-Hopf method is a powerful technique which enables certain linear partial differential equations subject to boundary conditions on semi-infinite domains to be solved explicitly. The method is sometimes referred to as the Wiener-Hopf technique or the Wiener-Hopf factorization.

The Wiener-Hopf method begins by applying the generalized upper and lower Fourier transforms to obtain an identity

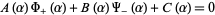(1)

on a strip

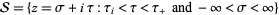(2)

of the complex 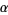-plane where  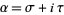is a complex variable. Note that identity () is in terms of the unknown functions  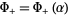and 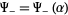 which are analytic in the half-planes  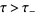and 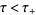, respectively, while 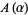, , 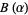and 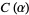 are "parameter functions" in the 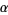-plane which are analytic on all of .

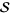For simplicity, assume that 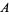 and 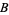 are non-zero in 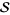. The most fundamental step of the Wiener-Hopf process is to find a solution for  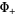and 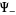 in () by finding functions  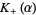and 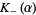--analytic and nonzero in  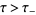and in 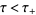, respectively--so that

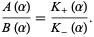(3)

Upon doing so, the factorization () can be used to rewrite () as

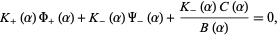(4)

whereby the last summand 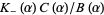 can be decomposed as

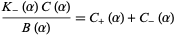(5)

for 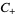, respectively 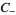, analytic in the region of  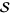satisfying 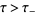, respectively .

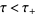Substituting () into () and rewriting induces a function 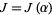 of the form

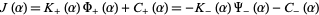(6)

which, despite being defined only in the strip 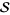, can be defined and made analytic on the entire complex 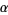-plane by way of analytic continuation. The idea behind () is to next show the existence of positive integers  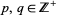for which

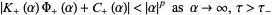(7)

and

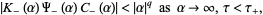(8)

whereby Liouville's theorem applies and requires that 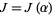 be a polynomial  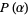of degree less than or equal to 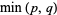. In particular,

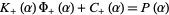(9)

and

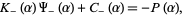(10)

thus defining 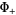 and 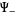 to within the arbitrary polynomial 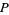, i.e., to within a finite number of arbitrary constants which must be determined using other methods.

While the Wiener-Hopf method itself is a useful tool for solving various types of partial differential equations, one of its most significant strengths is the vast array of other equation solving methods derived therefrom. Indeed, the techniques spawned from the Wiener-Hopf factorization have proven useful in a number of very different circumstances across a diverse array of disciplines including theoretical and applied physics (Noble 1958), diffraction theory (Linton and McIver 2001), and fluid dynamics (Ho 2007).

REFERENCES:

Ho, J. "The Wiener-Hopf Method and Its Applications in Fluids." 2007. http://www.ms.unimelb.edu.au/publications/HoJuwen.pdf.

Linton, C. M. and McIver, P. Handbook of Mathematical Techniques for Wave/Structure Interactions. Boca Raton, FL: CRC Press, 2001.

Noble, B. Methods Based on the Wiener-Hopf Technique For the Solution of Partial Differential Equations. Belfast, Northern Ireland: Pergamon Press, 1958.