
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-11-2018
Date: 11-12-2018
Date: 1-11-2018
|
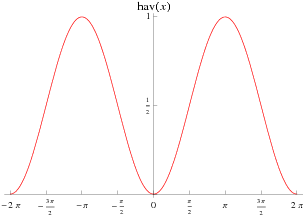
The haversine, also called the haversed sine, is a little-used entire trigonometric function defined by
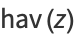 |
 |
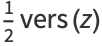 |
(1) |
 |
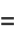 |
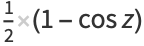 |
(2) |
 |
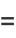 |
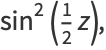 |
(3) |
where 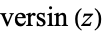 is the versine,
is the versine, 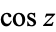 is the cosine, and
is the cosine, and 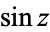 is the sine.
is the sine.
The haversine is implemented in the Wolfram Language as Haversine[z].
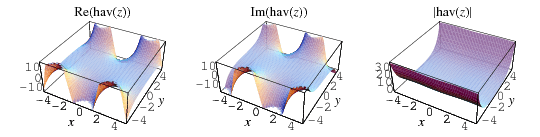
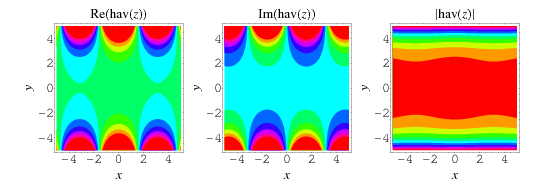
The haversine can be extended to the complex plane as illustrated above.
Its derivative is given by
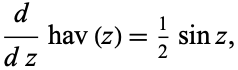 |
(4) |
and its indefinite integral by
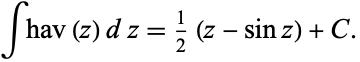 |
(5) |
It has Maclaurin series
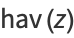 |
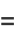 |
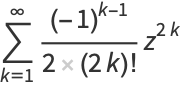 |
(6) |
 |
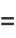 |
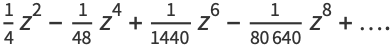 |
(7) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 78, 1972.
Smart, W. M. Text-Book on Spherical Astronomy, 6th ed. Cambridge, England: Cambridge University Press, p. 18, 1960.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|