Isoperimetric Problem

Find a closed plane curve of a given perimeter which encloses the greatest area. The solution is a circle. If the class of curves to be considered is limited to smooth curves, the isoperimetric problem can be stated symbolically as follows: find an arc with parametric equations 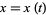,  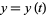for  such that 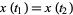,  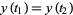(where no further intersections occur) constrained by

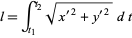such that

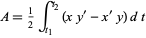is a maximum.

Zenodorus proved that the area of the circle is larger than that of any polygon having the same perimeter, but the problem was not rigorously solved until Steiner published several proofs in 1841 (Wells 1991).

REFERENCES:

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, p. 80, 2003.

Bogomolny, A. "Isoperimetric Theorem and Inequality." http://www.cut-the-knot.org/do_you_know/isoperimetric.shtml.

Isenberg, C. "The Maximum Area Contained by a Given Circumference." Appendix V in The Science of Soap Films and Soap Bubbles. New York: Dover, pp. 171-173, 1992.

Littlewood, J. E. Littlewood's Miscellany. Cambridge, England: Cambridge University Press, p. 32, 1986.

Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 149-150, 1999.

Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 122-124, 1991.