


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-6-2019
Date: 21-8-2018
Date: 23-4-2019
|
An identity in calculus of variations discovered in 1868 by Beltrami. The Euler-Lagrange differential equation is
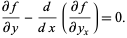 |
(1) |
Now, examine the derivative of 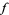 with respect to
with respect to 
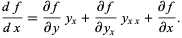 |
(2) |
Solving for the 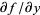 term gives
term gives
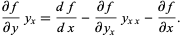 |
(3) |
Now, multiplying (1) by 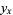 gives
gives
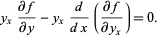 |
(4) |
Substituting (3) into (4) then gives
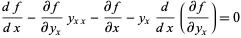 |
(5) |
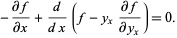 |
(6) |
This form is especially useful if 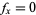 , since in that case
, since in that case
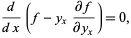 |
(7) |
which immediately gives
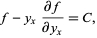 |
(8) |
where 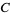 is a constant of integration (Weinstock 1974, pp. 24-25; Arfken 1985, pp. 928-929; Fox 1988, pp. 8-9).
is a constant of integration (Weinstock 1974, pp. 24-25; Arfken 1985, pp. 928-929; Fox 1988, pp. 8-9).
The Beltrami identity greatly simplifies the solution for the minimal area surface of revolution about a given axis between two specified points. It also allows straightforward solution of the brachistochrone problem.
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.
Fox, C. An Introduction to the Calculus of Variations. New York: Dover, 1988.
Weinstock, R. Calculus of Variations, with Applications to Physics and Engineering. New York: Dover, 1974.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|