


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-5-2019
Date: 2-10-2019
Date: 18-8-2019
|
Let lim stand for the limit 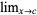 ,
, 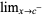 ,
, 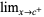 ,
, 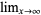 , or
, or 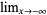 , and suppose that lim
, and suppose that lim 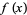 and lim
and lim 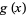 are both zero or are both
are both zero or are both 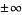 . If
. If
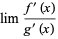 |
(1) |
has a finite value or if the limit is 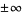 , then
, then
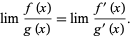 |
(2) |
Historically, this result first appeared in l'Hospital's 1696 treatise, which was the first textbook on differential calculus. Within the book, l'Hospital thanks the Bernoulli brothers for their assistance and their discoveries. An earlier letter by John Bernoulli gives both the rule and its proof, so it seems likely that Bernoulli discovered the rule (Larson et al. 1999, p. 524).
Note that l'Hospital's name is commonly seen spelled both "l'Hospital" (e.g., Maurer 1981, p. 426; Arfken 1985, p. 310) and "l'Hôpital" (e.g., Maurer 1981, p. 426; Gray 1997, p. 529), the two being equivalent in French spelling.
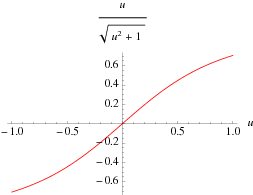
L'Hospital's rule occasionally fails to yield useful results, as in the case of the function 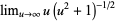 , illustrated above. Repeatedly applying the rule in this case gives expressions which oscillate and never converge,
, illustrated above. Repeatedly applying the rule in this case gives expressions which oscillate and never converge,
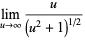 |
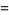 |
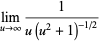 |
(3) |
 |
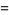 |
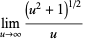 |
(4) |
 |
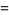 |
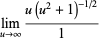 |
(5) |
 |
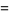 |
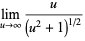 |
(6) |
 |
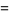 |
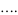 |
(7) |
The actual limit is 1.

L'Hospital's rule must sometimes be applied with some care, since it holds only in the implicitly understood case that 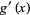 does not change sign infinitely often in a neighborhood of
does not change sign infinitely often in a neighborhood of  . For example, consider the limit
. For example, consider the limit 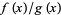 with
with
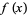 |
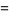 |
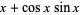 |
(8) |
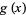 |
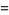 |
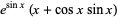 |
(9) |
as 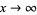 . While both
. While both 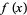 and
and 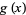 approach
approach 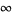 as
as  , the limit of the ratio is bounded inside the interval
, the limit of the ratio is bounded inside the interval ![[1/e,e]](http://mathworld.wolfram.com/images/equations/LHospitalsRule/Inline40.gif) , while the limit of
, while the limit of  approaches 0 (Boas 1986).
approaches 0 (Boas 1986).
Another similar example is the limit 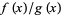 with
with
 |
 |
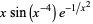 |
(10) |
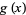 |
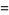 |
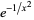 |
(11) |
as 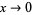 . While both
. While both 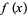 and
and 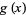 approach 0 as
approach 0 as 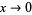 , the limit of the ratio is 0, while the limit
, the limit of the ratio is 0, while the limit 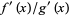 is unbounded on the real line (Wilf 1966, Rickert 1968).
is unbounded on the real line (Wilf 1966, Rickert 1968).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 13, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.
Boas, R. P. "Counterexamples to L'Hopital's Rule." Amer. Math. Monthly 93, 644-645, 1986.
Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.
Gruntz, D. In Computer Algebra Systems: A Practical Guide (Ed. M. J. Wester). Chichester, England: Wiley, 1999.
L'Hospital, G. de L'analyse des infiniment petits pour l'intelligence des lignes courbes. 1696.
Larson, R.; Hostetler, R. P.; and Edwards, B. H. Calculus: Early Transcendental Functions, 2nd ed. Boston: Houghton Mifflin, 1999.
Maurer, J. F. (Managing Ed.). Concise Dictionary of Scientific Biography. New York: Scribner's, 1981.
Rickert, N. W. "A Calculus Counterexample." Amer. Math. Monthly 75, 166, 1968.
Stolz, O. "Ueber die Grenzwerthe der Quotienten." Math. Ann. 15, 556-559, 1879.
Stolz, O. Grundzüge der Differential- und Integralrechnung, Vol. 1. Leipzig, Germany: Teubner, pp. 72-84, 1893.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, p. 60, 2004. http://www.mathematicaguidebooks.org/.
Wilf, H. S. Calculus and Linear Algebra. New York: Harcourt, Brace, and World, 1966.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|