


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-9-2018
Date: 27-4-2018
Date: 30-3-2019
|
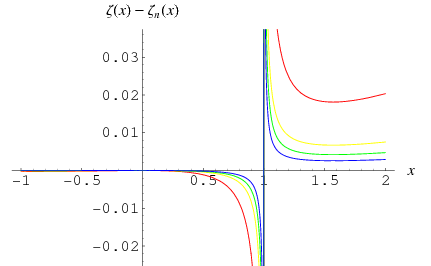
The Hadamard product is a representation for the Riemann zeta function 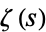 as a product over its nontrivial zeros
as a product over its nontrivial zeros 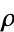 ,
,
![zeta(s)=(e^([ln(2pi)-1-gamma/2]s))/(2(s-1)Gamma(1+1/2s))product_(rho)(1-s/rho)e^(s/rho),](http://mathworld.wolfram.com/images/equations/HadamardProduct/NumberedEquation1.gif) |
(1) |
where 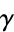 is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and 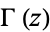 is the Gamma function (Titchmarsh 1987, Voros 1987). The constant in the exponent is given by
is the Gamma function (Titchmarsh 1987, Voros 1987). The constant in the exponent is given by
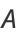 |
 |
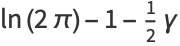 |
(2) |
 |
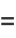 |
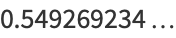 |
(3) |
(OEIS A077142). Hadamard used the Weierstrass product theorem to derive this result. The plot above shows the convergence of the formula along the real axis using the first 100 (red), 500 (yellow), 1000 (green), and 2000 (blue) Riemann zeta function zeros.
The product can also be stated in the alternate form
 |
(4) |
where 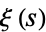 is the xi-function and
is the xi-function and
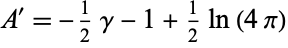 |
(5) |
(Havil 2003, p. 204).
REFERENCES:
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Sloane, N. J. A. Sequence A077142 in "The On-Line Encyclopedia of Integer Sequences."
Titchmarsh, E. C. The Theory of the Riemann Zeta Function, 2nd ed. New York: Clarendon Press, 1987.
Voros, A. "Spectral Functions, Special Functions and the Selberg Zeta Function." Commun. Math. Phys. 110, 439-465, 1987.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|