المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Vardi,s Integral |
 1675
 07:41 مساءً
date: 17-9-2018 |
Author : ailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H 
Book or Source : Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007. 
Page and Part : ...|
Read More
Date: 6-8-2019
4500
Date: 25-5-2019
2231
Date: 25-5-2019
1615
|
Vardi's integral is the beautiful definite integral
 |
 |
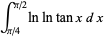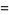![pi/2ln[sqrt(2pi)(Gamma(3/4))/(Gamma(1/4))]](http://mathworld.wolfram.com/images/equations/VardisIntegral/Inline3.gif) |
(1) |
 |
 |
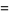![pi/4ln[(4pi^3)/(Gamma^4(1/4))]](http://mathworld.wolfram.com/images/equations/VardisIntegral/Inline6.gif) |
(2) |
 |
 |
 |
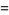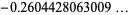(3) |
(OEIS A115252; Gradshteyn and Ryzhik 1980, p. 532; Bailey et al. 2007, p. 160; Moll 2006), where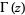 
is the gamma function.
Other examples similar to these include
 |
 |
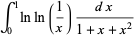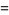![pi/(sqrt(3))ln[(2pi^(5/6))/(Gamma(1/6))]](http://mathworld.wolfram.com/images/equations/VardisIntegral/Inline13.gif) |
(4) |
 |
 |
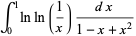![pi/(sqrt(3))ln[(32pi^5)/(Gamma^6(1/6))]](http://mathworld.wolfram.com/images/equations/VardisIntegral/Inline16.gif) |
(5) |
(Vardi 1988; Gradshteyn and Ryzhik 1980, pp. 571-572).
REFERENCES:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Bierens de Haan, D. Nouvelles Tables d'intégrales définies. Amsterdam, 1867.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 4th ed. San Diego, CA: Academic Press, 1980.
Moll, V. H. "Some Questions in the Evaluation of Definite Integrals." MAA Short Course, San Antonio, TX. Jan. 2006. http://crd.lbl.gov/~dhbailey/expmath/maa-course/Moll-MAA.pdf.
Sloane, N. J. A. Sequence A115252 in "The On-Line Encyclopedia of Integer Sequences."
Vardi, I. "Integrals, an Introduction to Analytic Number Theory." Amer. Math. Monthly 95, 308-315, 1988.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|
