


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-8-2018
Date: 26-8-2019
Date: 14-5-2018
|
 |
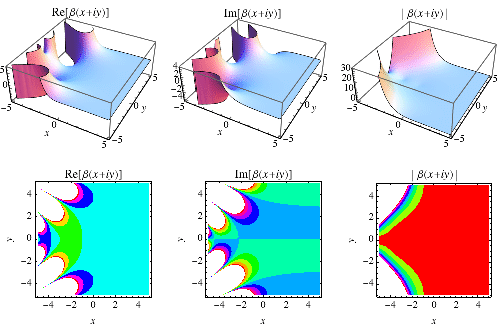 |
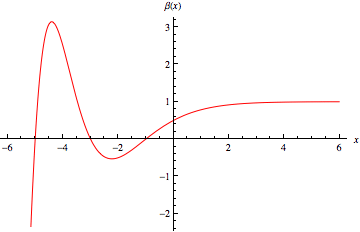
The Dirichlet beta function is defined by the sum
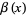 |
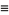 |
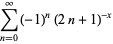 |
(1) |
 |
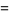 |
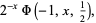 |
(2) |
where 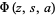 is the Lerch transcendent. The beta function can be written in terms of the Hurwitz zeta function
is the Lerch transcendent. The beta function can be written in terms of the Hurwitz zeta function 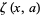 by
by
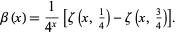 |
(3) |
The beta function can be defined over the whole complex plane using analytic continuation,
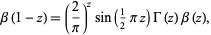 |
(4) |
where 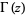 is the gamma function.
is the gamma function.
The Dirichlet beta function is implemented in the Wolfram Language as DirichletBeta[x].
The beta function can be evaluated directly special forms of arguments as
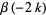 |
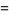 |
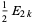 |
(5) |
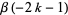 |
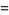 |
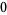 |
(6) |
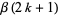 |
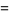 |
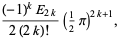 |
(7) |
where 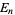 is an Euler number.
is an Euler number.
Particular values for 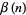 are
are
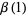 |
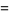 |
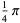 |
(8) |
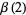 |
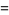 |
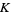 |
(9) |
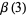 |
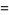 |
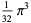 |
(10) |
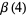 |
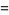 |
![1/(768)[psi_3(1/4)-8pi^4],](http://mathworld.wolfram.com/images/equations/DirichletBetaFunction/Inline32.gif) |
(11) |
where 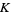 is Catalan's constant and
is Catalan's constant and 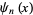 is the polygamma function. For
is the polygamma function. For 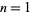 , 3, 5, ...,
, 3, 5, ..., 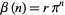 , where the multiples are 1/4, 1/32, 5/1536, 61/184320, ... (OEIS A046976 and A053005).
, where the multiples are 1/4, 1/32, 5/1536, 61/184320, ... (OEIS A046976 and A053005).
It is involved in the integral
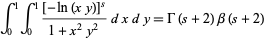 |
(12) |
(Guillera and Sondow 2005).
Rivoal and Zudilin (2003) proved that at least one of the seven numbers 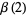 ,
, 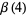 ,
, 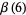 ,
, 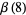 ,
, 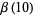 ,
, 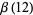 , and
, and 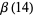 is irrational.
is irrational.
The derivative 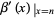 can also be computed analytically at a number of integer values of
can also be computed analytically at a number of integer values of 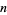 including
including
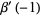 |
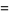 |
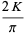 |
(13) |
 |
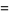 |
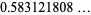 |
(14) |
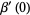 |
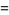 |
![ln[(Gamma^2(1/4))/(2pisqrt(2))]](http://mathworld.wolfram.com/images/equations/DirichletBetaFunction/Inline54.gif) |
(15) |
 |
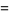 |
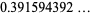 |
(16) |
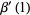 |
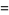 |
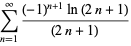 |
(17) |
 |
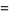 |
![1/4pi{gamma+2ln2+3lnpi-4ln[Gamma(1/4)]}](http://mathworld.wolfram.com/images/equations/DirichletBetaFunction/Inline63.gif) |
(18) |
 |
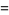 |
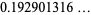 |
(19) |
(OEIS A133922, A113847, and A078127), where 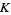 is Catalan's constant,
is Catalan's constant, 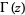 is the gamma function, and
is the gamma function, and 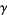 is the Euler-Mascheroni constant.
is the Euler-Mascheroni constant.
A nice sum involving 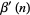 is given by
is given by
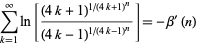 |
(20) |
for 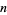 a positive integer.
a positive integer.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 807-808, 1972.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, p. 384, 1987.
Comtet, L. Problem 37 in Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, p. 89, 1974.
Guillera, J. and Sondow, J. "Double Integrals and Infinite Products for Some Classical Constants Via Analytic Continuations of Lerch's Transcendent." 16 June 2005 http://arxiv.org/abs/math.NT/0506319.
Rivoal, T. and Zudilin, W. "Diophantine Properties of Numbers Related to Catalan's Constant." Math. Ann. 326, 705-721, 2003. http://www.mi.uni-koeln.de/~wzudilin/beta.pdf.
Sloane, N. J. A. Sequences A046976, A053005, A078127, A113847, and A133922 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Zeta Numbers and Related Functions." Ch. 3 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 25-33, 1987.
Mathews, J. and Walker, R. L. Mathematical Methods of Physics, 2nd ed. Reading, MA: W. A. Benjamin/Addison-Wesley, p. 57, 1970.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|