Helmholtz Differential Equation--Prolate Spheroidal Coordinates

As shown by Morse and Feshbach (1953) and Arfken (1970), the Helmholtz differential equation is separable in prolate spheroidal coordinates.

REFERENCES:

Arfken, G. "Prolate Spheroidal Coordinates 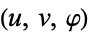." §2.10 in Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 103-107, 1970.

Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, pp. 243-244, 1959.

Moon, P. and Spencer, D. E. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed.New York: Springer-Verlag, p. 30, 1988.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 661, 1953.