
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-6-2018
Date: 22-6-2018
Date: 21-5-2018
|
Let 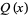 be a real or complex piecewise-continuous function defined for all values of the real variable
be a real or complex piecewise-continuous function defined for all values of the real variable  and that is periodic with minimum period
and that is periodic with minimum period 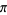 so that
so that
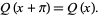 |
(1) |
Then the differential equation
 |
(2) |
has two continuously differentiable solutions 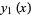 and
and 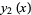 , and the characteristic equation is
, and the characteristic equation is
 |
(3) |
with eigenvalues 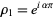 and
and 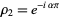 . Then Floquet's theorem states that if the roots
. Then Floquet's theorem states that if the roots 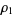 and
and 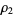 are different from each other, then (2) has two linearly independent solutions
are different from each other, then (2) has two linearly independent solutions
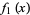 |
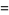 |
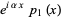 |
(4) |
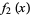 |
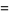 |
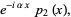 |
(5) |
where 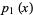 and
and 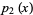 are periodic with period
are periodic with period 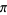 (Magnus and Winkler 1979, p. 4).
(Magnus and Winkler 1979, p. 4).
REFERENCES:
Magnus, W. and Winkler, S. "Floquet's Theorem." §1.2 in Hill's Equation. New York: Dover, pp. 3-8, 1979.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|