Density functional theory
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص395-396
2025-11-30
13
Density functional theory
A technique that has gained considerable ground in recent years to become one of the most widely used techniques for the calculation of molecular structure is density functional theory (DFT). Its advantages include less demanding computational effort, less computer time, and—in some cases (particularly d-metal complexes)—better agree ment with experimental values than is obtained from Hartree–Fock procedures. The central focus of DFT is the electron density, ρ, rather than the wavefunction ψ. The ‘functional’ part of the name comes from the fact that the energy of the molecule is a function of the electron density, written E[ρ], and the electron density is itself a function of position, ρ(r), and in mathematics a function of a function is called a functional. The exact ground-state energy of an n-electron molecule is , E[ρ]=EK+EP;e,N+EP;e,e+EXC[ρ] , Where EK is the total electron kinetic energy, EP;e,Nthe electron–nucleus potential energy, EP;e,e the electron–electron potential energy, and EXC[ρ] the exchange correlation energy, which takes into account all the effects due to spin. The orbitals used to construct the electron density from
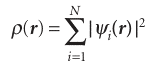
are calculated from the Kohn–Sham equations, which are found by applying the variation principle to the electron energy, and are like the Hartree–Fock equations except for a term VXC, which is called the exchange–correlation potential:
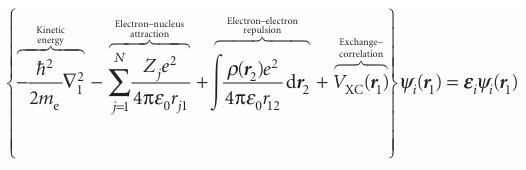
The exchange–correlation potential is the ‘functional derivative’ of the exchange correlation energy:
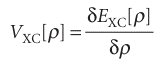
The Kohn–Sham equations are solved iteratively and self-consistently. First, we guess the electron density. For this step it is common to use a superposition of atomic electron densities. Then the exchange–correlation potential is calculated by assuming an approximate form of the dependence of the exchange–correlation energy on the electron density and evaluating the functional derivative in eqn 11.61. For this step, the simplest approximation is the local-density approximation and to write
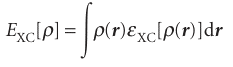
where εXC is the exchange–correlation energy per electron in a homogeneous gas of constant density. Next, the Kohn–Sham equations are solved to obtain an initial set of orbitals. This set of orbitals is used to obtain a better approximation to the electron density (from eqn 11.59) and the process is repeated until the density and the exchange–correlation energy are constant to within some tolerance.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
