Semi-empirical and ab initio methods
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص394-395
2025-11-30
6
Semi-empirical and ab initio methods
There are two main strategies for continuing the calculation from this point. In the semi-empirical methods, many of the integrals are estimated by appealing to spectroscopic data or physical properties such as ionization energies, and using a series of rules to set certain integrals equal to zero. In the ab initiomethods, an attempt is made to calculate all the integrals that appear in the Fock and overlap matrices. Both procedures employ a great deal of computational effort and, along with cryptanalysts and meteorologists, theoretical chemists are among the heaviest users of the fastest computers. The Fock matrix has elements that consist of integrals of the form
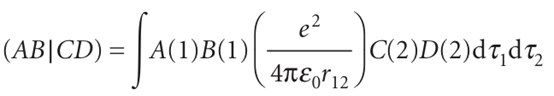
Where A,B,C, and Dare atomic orbitals that in general may be centred on different nuclei. It can be appreciated that, if there are several dozen atomic orbitals used to build the molecular orbitals, then there will be tens of thousands of integrals of this form to evaluate (the number of integrals increases as the fourth power of the number of atomic orbitals in the basis). One severe approximation is called complete neglect of differential overlap (CNDO), in which all integrals are set to zero unless AandB are the same orbitals centred on the same nucleus, and likewise for CandD. The surviving integrals are then adjusted until the energy levels are in good agreement with experiment. The more recent semi-empirical methods make less draconian decisions about which integrals are to be ignored, but they are all descendants of the early CNDO technique. These procedures are now readily available in commercial software packages and can be used with very little detailed knowledge of their mode of calculation. The packages also have sophisticated graphical output procedures, which enable one to analyse the shapes of orbitals and the distribution of electric charge in molecules. The latter is important when assessing, for instance, the likelihood that a given molecule will bind to an active site in an enzyme. Commercial packages are also available for ab initio calculations. Here the problem is to evaluate as efficiently as possible thousands of integrals. This task is greatly facilitated by expressing the atomic orbitals used in the LCAOs as linear combinations of Gaussian orbitals. A Gaussian type orbital (GTO) is a function of the form e−ζr2. The advantage of GTOs over the correct orbitals (which for hydrogenic systems are proportional to e−ζr) is that the product of two Gaussian functions is itself a Gaussian function that lies between the centres of the two contributing functions (Fig. 11.42). In this way, the four-centre integrals like that in eqn 11.56 become two-centre integrals of the form
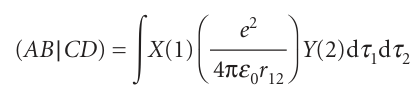
Where X is the Gaussian corresponding to the product AB and Y is the corresponding Gaussian from CD. Integrals of this form are much easier and faster to evaluate numeric ally than the original four-centre integrals. Although more GTOs have to be used to simulate the atomic orbitals, there is an overall increase in speed of computation.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
