The solid–liquid boundary
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص126-127
2025-11-11
33
The solid–liquid boundary
Melting (fusion) is accompanied by a molar enthalpy change ∆fusH and occurs at a temperature T. The molar entropy of melting at T is therefore ∆fusH/T (Section 3.3), and the Clapeyron equation becomes
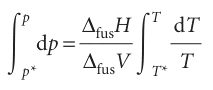
where ∆fusV is the change in molar volume that occurs on melting. The enthalpy of melting is positive (the only exception is helium-3) and the volume change is usually positive and always small. Consequently, the slope dp/dT is steep and usually positive (Fig. 4.13). We can obtain the formula for the phase boundary by integrating dp/dT, assuming that ∆fusH and ∆fusV change so little with temperature and pressure that they can be treated as constant. If the melting temperature is T* when the pressure is p*, and T when the pressure is p, the integration required is
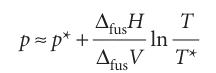
Therefore, the approximate equation of the solid–liquid boundary is
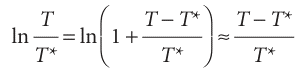
This equation was originally obtained by yet another Thomson—James, the brother of William, Lord Kelvin. When T is close to T*, the logarithm can be approximated by using
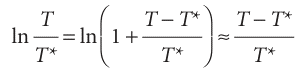
therefore,
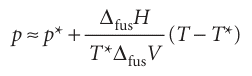
This expression is the equation of a steep straight line when p is plotted against T (as in Fig. 4.13).
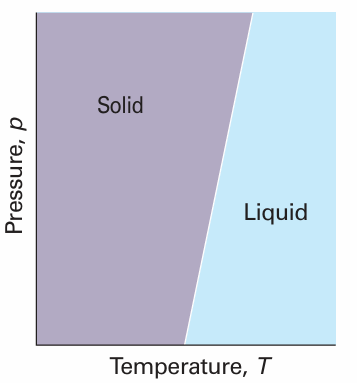
Fig. 4.13 A typical solid–liquid phase boundary slopes steeply upwards. This slope implies that, as the pressure is raised, the melting temperature rises. Most substances behave in this way.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
