The slopes of the phase boundaries
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
126
2025-11-11
27
The slopes of the phase boundaries
It turns out to be simplest to discuss the phase boundaries in terms of their slopes, dp/dT. Let p and T be changed infinitesimally, but in such a way that the two phases α and βremain in equilibrium. The chemical potentials of the phases are initially equal (the two phases are in equilibrium). They remain equal when the conditions are changed to another point on the phase boundary, where the two phases continue to be in equilibrium (Fig. 4.12). Therefore, the changes in the chemical potentials of the two phases must be equal and we can write dµα = dµβ. Because, from eqn 3.49 (dG = Vdp−SdT), we know that dµ =−Sm dT + Vmdp for each phase, it follows that
−Sα,mdT + Vα,mdp =−Sβ,mdT+Vβ,mdp
where Sα,m and Sβ,m are the molar entropies of the phases and Vα,m and Vβ,m are their molar volumes. Hence
(Vβ,m − Vα,m)dp = (Sβ,m − Sα,m)dT
which rearranges into the Clapeyron equation:
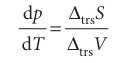
In this expression ∆trsS = Sβ,m − Sα,m and ∆trsV = Vβ,m − Vα,m are the entropy and volume of transition, respectively. The Clapeyron equation is an exact expression for the slope of the phase boundary and applies to any phase equilibrium of any pure sub stance. It implies that we can use thermodynamic data to predict the appearance of phase diagrams and to understand their form. A more practical application is to the prediction of the response of freezing and boiling points to the application of pressure.
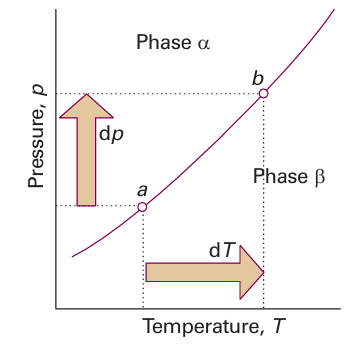
Fig. 4.12 When pressure is applied to a system in which two phases are in equilibrium (at a), the equilibrium is disturbed. It can be restored by changing the temperature, so moving the state of the system to b. It follows that there is a relation between dp and dT that ensures that the system remains in equilibrium as either variable is changed.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
