The effect of applied pressure on vapour pressure
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص124-125
2025-11-11
36
The effect of applied pressure on vapour pressure
When pressure is applied to a condensed phase, its vapour pressure rises: in effect, molecules are squeezed out of the phase and escape as a gas. Pressure can be exerted on the condensed phases mechanically or by subjecting it to the applied pressure of an inert gas (Fig. 4.11); in the latter case, the vapour pressure is the partial pressure of the vapour in equilibrium with the condensed phase, and we speak of the partial vapour pressure of the substance. One complication (which we ignore here) is that, if the condensed phase is a liquid, then the pressurizing gas might dissolve and change the properties of the liquid. Another complication is that the gas phase molecules might attract molecules out of the liquid by the process of gas solvation, the attachment of molecules to gas phase species. As shown in the following Justification, the quantitative relation between the vapour pressure, p, when a pressure ∆P is applied and the vapour pressure, p*, of the liquid in the absence of an additional pressure is
p =p*eVm(l)∆P/RT
This equation shows how the vapour pressure increases when the pressure acting on the condensed phase is increased.
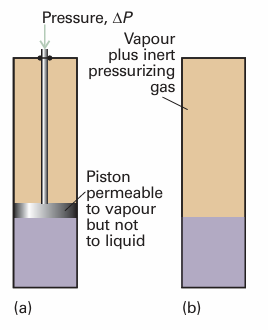
Fig. 4.11 Pressure may be applied to a condensed phases either (a) by compressing the condensed phase or (b) by subjecting it to an inert pressurizing gas. When pressure is applied, the vapour pressure of the condensed phase increases.
Justification 4.1 The vapour pressure of a pressurized liquid We calculate the vapour pressure of a pressurized liquid by using the fact that at equilibrium the chemical potentials of the liquid and its vapour are equal: µ(l) = µ(g). It follows that, for any change that preserves equilibrium, the resulting change in µ(l) must be equal to the change in µ(g); therefore, we can write dµ(g) = dµ(l). When the pressure P on the liquid is increased by dP, the chemical potential of the liquid changes by dµ(l) = Vm(l)dP. The chemical potential of the vapour changes by dµ(g)=Vm(g)dp where dp is the change in the vapour pressure we are trying to find. If we treat the vapour as a perfect gas, the molar volume can be replaced by Vm(g) = RT/p, and we obtain
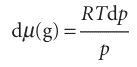
Next, we equate the changes in chemical potentials of the vapour and the liquid:
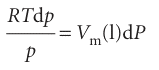
We can integrate this expression once we know the limits of integration. When there is no additional pressure acting on the liquid, P (the pressure experienced by the liquid) is equal to the normal vapour pressure p*, so when P = p*, p = p* too. When there is an additional pressure ∆P on the liquid, with the result that P=p+∆P, the vapour pressure is p (the value we want to find). Provided the effect of pressure on the vapour pressure is small (as will turn out to be the case) a good approximation is to replace the p in p +∆P by p* itself, and to set the upper limit of the integral to p* +∆P. The integrations required are therefore as follows:
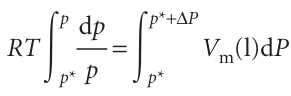
We now divide both sides by RT and assume that the molar volume of the liquid is the same throughout the small range of pressures involved:
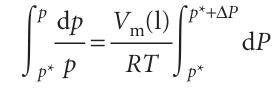
Then both integrations are straightforward, and lead to
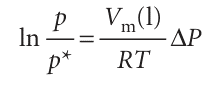
which rearranges to eqn 4.3 because elnx = x.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
