B-Spline
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
www.almerja.com
الجزء والصفحة:
...
18-11-2021
1607
B-Spline
A B-spline is a generalization of the Bézier curve. Let a vector known as the knot vector be defined
![T=<span style=]() {t_0,t_1,...,t_m}, " src="https://mathworld.wolfram.com/images/equations/B-Spline/NumberedEquation1.gif" style="height:15px; width:110px" /> |
(1)
|
where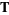 
is a nondecreasing sequence with ![t_i in [0,1]](https://mathworld.wolfram.com/images/equations/B-Spline/Inline2.gif)
, and define control points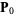 
, ..., 
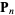. Define the degree as
 |
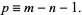(2)
|
The "knots"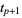 
, ..., 
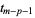are called internal knots.
Define the basis functions as
where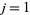 
, 2, ..., 
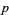. Then the curve defined by
 |
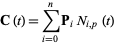(5)
|
is a B-spline.
Specific types include the nonperiodic B-spline (first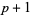 
knots equal 0 and last 
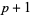equal to 1; illustrated above) and uniform B-spline (internal knots are equally spaced). A B-spline with no internal knots is a Bézier curve.
A curve is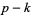 
times differentiable at a point where 
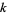duplicate knot values occur. The knot values determine the extent of the control of the control points.
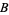-splines are implemented in the Wolfram Language as BSplineCurve[pts].
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
