Arnold,s Cat Map
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
www.almerja.com
الجزء والصفحة:
...
6-10-2021
1442
Arnold's Cat Map
The best known example of an Anosov diffeomorphism. It is given by the transformation
![[x_(n+1); y_(n+1)]=[1 1; 1 2][x_n; y_n],](https://mathworld.wolfram.com/images/equations/ArnoldsCatMap/NumberedEquation1.gif) |
(1)
|
where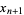 
and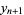 
are computed mod 1. The Arnold cat mapping is non-Hamiltonian, nonanalytic, and mixing. However, it is area-preserving since the determinant is 1. The Lyapunov characteristic exponents are given by
 |
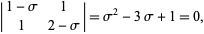(2)
|
so
 |
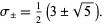(3)
|
The eigenvectors are found by plugging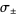 
into the matrix equation
![[1-sigma_+/- 1; 1 2-sigma_+/-][x; y]=[0; 0].](https://mathworld.wolfram.com/images/equations/ArnoldsCatMap/NumberedEquation4.gif) |
(4)
|
For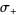 
, the solution is
 |
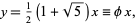(5)
|
where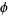 
is the golden ratio, so the unstable (normalized) eigenvector is
![xi_+=1/(10)sqrt(50-10sqrt(5))[1; 1/2(1+sqrt(5))].](https://mathworld.wolfram.com/images/equations/ArnoldsCatMap/NumberedEquation6.gif) |
(6)
|
Similarly, for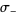 
, the solution is
 |
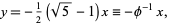(7)
|
so the stable (normalized) eigenvector is
![xi_-=1/(10)sqrt(50+10sqrt(5))[1; 1/2(1-sqrt(5))].](https://mathworld.wolfram.com/images/equations/ArnoldsCatMap/NumberedEquation8.gif) |
(8)
|
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
