Filter
المؤلف:
Hamming, R. W
المصدر:
Digital Filters. New York: Dover, 1998.
الجزء والصفحة:
...
28-9-2021
1346
Filter
Let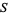 
be a nonempty set, then a filter on 
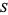is a nonempty collection 
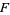of subsets of 
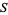having the following properties:
1. 
,
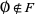2. If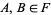 
, then 
,
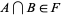3. If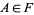 
and 
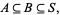then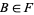 
If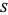 
is an infinite set, then the collection ![F_S=<span style=]()
{A subset= S:S-A is finite}" src="https://mathworld.wolfram.com/images/equations/Filter/Inline12.gif" style="height:15px; width:161px" /> is a filter called the cofinite (or Fréchet) filter on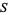 
.
In signal processing, a filter is a function or procedure which removes unwanted parts of a signal. The concept of filtering and filter functions is particularly useful in engineering. One particularly elegant method of filtering Fourier transforms a signal into frequency space, performs the filtering operation there, then transforms back into the original space (Press et al. 1992).
REFERENCES:
Hamming, R. W. Digital Filters. New York: Dover, 1998.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Digital Filtering in the Time Domain." §13.5 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 551-556, 1992.
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
