Reverend Back,s Abbey Floor
المؤلف:
Allouche, J.-P. and Shallit, J.
المصدر:
Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press, 2003.
الجزء والصفحة:
...
25-9-2021
1813
Reverend Back's Abbey Floor
Consider the sequence defined by 
and 
, where 
denotes the reverse of a sequence 
. The first few terms are then 01, 010110, 010110010110011010, .... All words 
are cubefree (Allouche and Shallit 2003, p. 28, Ex. 1.49). Iterating gives the sequence 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, ... (OEIS A118006)
Plotting 
(mod 2), where 
denotes the 
th digit of the infinitely iterated sequence, gives the beautiful pattern shown above, known as Reverend Back's abbey floor (Wegner 1982; Siromoney and Subramanian 1983; Allouche and Shallit 2003, pp. 410-411). Note that this plot is identical to the recurrence plot 
(mod 2).
REFERENCES:
Allouche, J.-P. and Shallit, J. Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press, 2003.
Siromoney, R. and Subramanian, K. G. "Generative Grammar for the Cube-Free Abbey Floor." Bull. Eur. Assoc. Theor. Comput. Sci., No. 20, 160-162, Jun. 1983.
Sloane, N. J. A. Sequence A118006 in "The On-Line Encyclopedia of Integer Sequences."
Wegner, L. "Problem P12: Is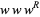 
Cube-Free?" Bull. Eur. Assoc. Theor. Comput. Sci., No. 18, 120, Oct. 1982.
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
