


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-3-2017
Date: 14-3-2017
Date: 12-3-2017
|
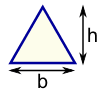 |
Triangle |
|
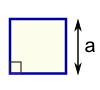 |
Square |
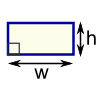 |
Rectangle |
|
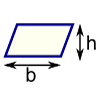 |
Parallelogram |
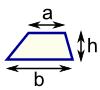 |
Trapezoid (US) |
|
 |
Circle |
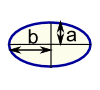 |
Ellipse |
|
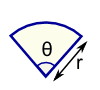 |
Sector |
|
Note: h is at right angles to b: |
|
|
Example: What is the area of this rectangle?
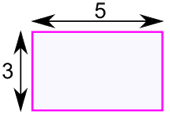
The formula is:
Area = w × h
w = width
h = height
We know w = 5 and h = 3, so:
Area = 5 × 3 = 15
Example: What is the area of this circle?
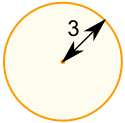
Radius = r = 3
|
Area |
|
= π × r2 |
|
|
|
= π × 32 |
|
|
|
= π × (3 × 3) |
|
|
|
= 3.14159... × 9 |
|
|
|
= 28.27 (to 2 decimal places) |
|
|
|
|
Example: What is the area of this triangle?
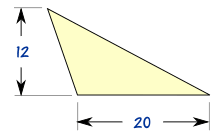
Height = h = 12
Base = b = 20
Area = ½ × b × h = ½ × 20 × 12 = 120
A harder example:
Example: Sam cuts grass at $0.10 per square meter
How much does Sam earn cutting this area:
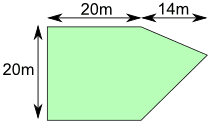
Let's break the area into two parts:
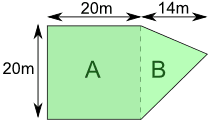
Part A is a square:
Area of A = a2 = 20m × 20m = 400m2
Part B is a triangle. Viewed sideways it has a base of 20m and a height of 14m.
Area of B = ½b × h = ½ × 20m × 14m = 140m2
So the total area is:
Area = Area of A + Area of B = 400m2 + 140m2 = 540m2
Sam earns $0.10 per square meter
Sam earns = $0.10 × 540m2 = $54



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|