


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-2-2017
Date: 8-2-2017
Date: 13-2-2017
|
Trigonometric equations. Main methods for solving
Trigonometric equations. Simplest trigonometric equations.
Methods of solving: algebraic method, factoring, reducing
to a homogeneous equation, transition to a half-angle,
introducing an auxiliary angle, transforming a product to
a sum, universal substitution.
Trigonometric equations. An equation, containing an unknown under the trigonometric function sign is called trigonometric.
Simplest trigonometric equations.

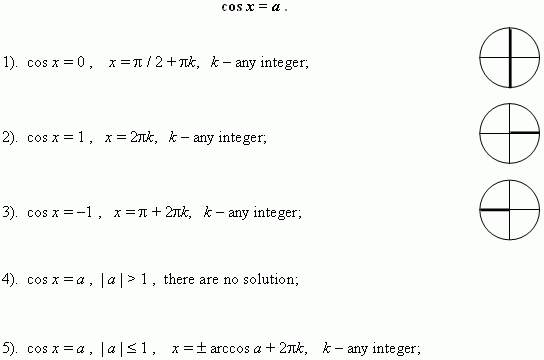

Methods for solving trigonometric equations. Solving of a trigonometric equation consists of the two stages: transforming of a equation to receive its simplest shape ( see above ) and solving of the received simplest trigonometric equation. There are seven main methods of solution of trigonometric equations.
1. Algebraic method. This method is well known for us from algebra ( exchange and
substitution method ).
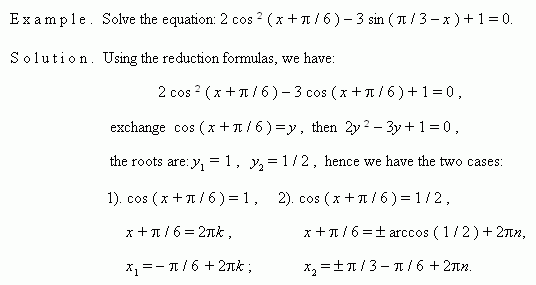
2. Factoring. Consider this method by examples.
E x a m p l e 1. Solve the equation: sin x + cos x = 1 .
S o l u t i o n . Transfer all terms to the left:
sin x + cos x – 1 = 0 ,
transform and factor the left-hand side expression:
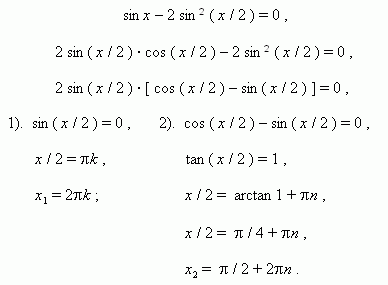
E x a m p l e 2. Solve the equation: cos² x + sin x · cos x = 1.
S o l u t i o n . cos ² x + sin x · cos x – sin ² x – cos ² x = 0 ,
sin x · cos x – sin ² x = 0 ,
sin x · ( cos x – sin x ) = 0 ,
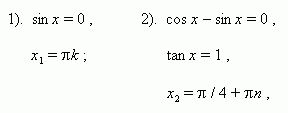
E x a m p l e 3. Solve the equation: cos 2x – cos 8x + cos 6x = 1.
S o l u t i o n . cos 2x + cos 6x = 1 + cos 8x ,
2 cos 4x cos 2x = 2 cos ² 4x ,
cos 4x · ( cos 2x – cos 4x ) = 0 ,
cos 4x · 2 sin 3x · sin x = 0 ,
1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,
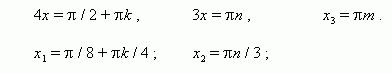
|
3. |
Reducing to a homogeneous equation. An equation is called a homogeneous equation in sin and cos, if and only if all its terms are of the same degree in sin and cos of the same angle. E x a m p l e . Solve the equation: 3 sin ² x + 4 sin x · cos x + 5 cos ² x = 2. S o l u t i o n . 3 sin ² x + 4 sin x · cos x + 5 cos ² x = 2sin ² x + 2cos ² x , sin ² x + 4 sin x · cos x + 3 cos ² x = 0 , tan ² x + 4 tan x + 3 = 0 , hence y ² + 4y +3 = 0 , the roots of this equation are: y1 = –1 , y2 = –3 , from here 1) tan x = –1, 2) tan x = –3, |
4. Transition to a half-angle. Consider this method by the example:
E x a m p l e . Solve the equation: 3 sin x – 5 cos x = 7.
S o l u t i o n . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =
= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,
2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,
tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,
. . . . . . . . . .
5. Introducing an auxiliary angle. Consider an equation of the shape:
a sin x + b cos x = c ,
where a, b, c – coefficients; x – an unknown.
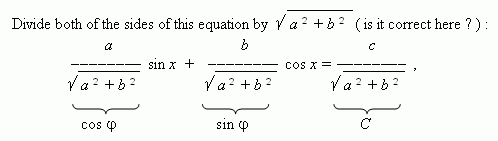
New coefficients in the left-hand side have the properties of sine and cosine: a modulus
( absolute value ) of each of them is not more than 1, and a sum of their squares is equal
to 1. So, we can mark them as cos φ and sin φ correspondingly; here  is the so called
is the so called
an auxiliary angle.
Now our equation has the shape:
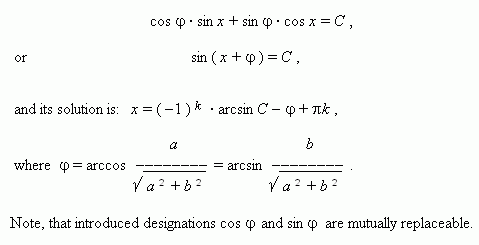
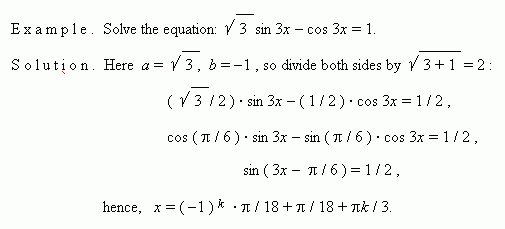
6. Transforming a product to a sum. The corresponding formulas are used here.
E x a m p l e . Solve the equation: 2 sin 2x · sin 6x = cos 4x.
S o l u t i o n . Transform the left-hand side to the sum:
cos 4x – cos 8x = cos 4x ,
cos 8x = 0 ,
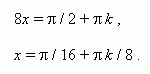
7. Universal substitution. Consider this method by example.
E x a m p l e . Solve the equation: 3 sin x – 4 cos x = 3 .

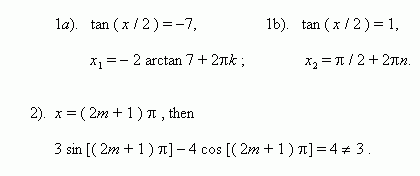
So, only the first case gives the solution.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|