


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 24-1-2017
Date: 18-8-2020
Date: 22-11-2020
|
Speckle interferometry
Detailed descriptions of (infrared) speckle interferometry and imaging have been given in several reviews (Christou 1991, Roddier 1989, Mariotti 1989, Dainty 1975). Here I only give a brief summary in order to introduce expressions that are linked to this technique and that are used in the following description of the data reduction and interpretation. The atmospheric turbulence above the telescope distorts the otherwise plane stellar wavefronts and is responsible for a point spread function that varies rapidly with time. This phenomenon is called seeing. Over entities of the turbulent layer seeing cells with a Fried (1966) diameter r0 ∼ 20–50 cm in the near-infrared (NIR)—the phase front predominantly experiences a linear phase change only. Neighouring stars within the isoplanatic patch of about a 20–30'' diameter in the NIR have a similar resulting PSF (point spread function) within the coherence time of the atmosphere (up to a few 100 ms in the NIR).
An image I (x, y) of an object O(x, y) taken in the focal plane (with coordinates x and y) through the combination of the telescope and the turbulent atmosphere can be written as the convolution of O(x, y) with the combined telescope and atmospheric PSF P(x, y):
I (x, y) = O(x, y) ∗ P(x, y). (1.1)
Co adding all short exposures after shifting the positions of the brightest speckle in the seeing cloud I (x, y) of a bright reference object to a common location results in an image containing substantial power at the diffraction limit of the telescope. The speckle image processing can formally be described in the following way: two-dimensional images I (x, y) can be written as the object O(x, y) convolved with the combined telescope and atmospheric PSF P(x, y) plus an additive noise component N(x, y),
I (x, y) = O(x, y) ∗ P(x, y) + N(x, y). (1.2)
In the simple shift-and-add algorithm one determines the location of the brightest speckle in the seeing disk of a reference star in each of the M images Im(x, y) of a series of short exposures and shifts them to the same position before summing the images:
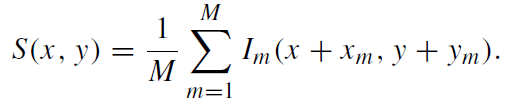 (1.3)
(1.3)
The xm and ym are the corresponding shift vector components. One obtains a shift and add image S(x, y) that can be written as the object convolved with a shift and add PSF Ps(x, y) plus a modified noise contribution Ns(x, y):
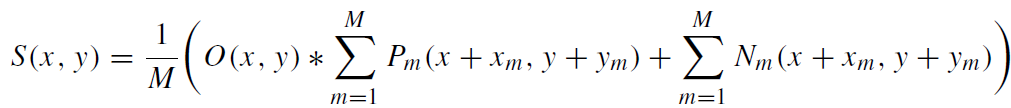 (1.4)
(1.4)
or
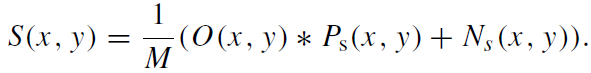 (1.5)
(1.5)
For each star in the field of view (smaller than the isoplanatic patch size) this PSF results in a diffraction-limited image of the object on top of a residual seeing background built up by the contributions from all fainter speckles. In contrast to the long exposure (a simple co-addition of individual frames) the raw shift and add image contains information at the diffraction limit of the telescope. In the NIR and especially for the Galactic Center observations the shift and ad algorithm has the following advantages over the other well-known speckle reduction algorithms which are based on a Fourier analysis of the images like the Knox-Thompson method and bi-spectrum analysis: (1) no Fourier transforms have to be involved resulting in a fast processing of a large amount of data; and (2) local artifacts in the image plane are not spread all over the Fourier plane making it easier to employ deconvolution methods especially if the bright supergiant IRS 7 is in the same field of view as the Sgr A∗ region.
After application of the shift-and-add algorithm the resulting images contain up to approximately 20% of the image power at the diffraction limit but they still have to be corrected for the PSF produced by the shift-and-add algorithm. In the data reduction scheme presented here this is done using the Lucy algorithm (Lucy 1974). This correction aims at replacing the PSF of the shift-and-add algorithm that contains a broad seeing pedestal in addition to a diffraction-limited core with a single Gaussian-shaped PSF.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|