For the present, we will limit our discussion to the simplest kinds of circuits, those involving only switches. We will designate a switch by a single letter a, b, c, x, y, .. .  If two switches operate so that they open and close simultaneously, we designate them by the same letter. If they operate so that the first is always open when the second is closed, and closed when the second is open, we denote the first by a letter, say x, and the second by x' (or,  equally well, the first by x' and the second by x).  A circuit consisting of two switches x and y connected in parallel is denoted by x + y, and a circuit consisting of x and y connected in series is denoted by xy. Thus to each series-parallel circuit, there corresponds an algebraic expression; and conversely to each algebraic expression

Fig. 1-1. Correspondence functions with circuits.

involving only (-), (.)and ('), there corresponds a circuit (see Fig. 1-1).

We will speak of this relationship by saying that the function represents the circuit, and the circuit realizes the function.

We will agree to assign the value 1 to a letter if it represents a closed switch, and the value 0 if it represents an open switch. If a and a' both appear, then a is 1 if and only if a' is 0. A switch that is always closed is represented by 1, one that is always open by 0. Letters play the role of variables which take on the value 0 or 1, and we note the close analogy to proposition variables, which have the same possible values, although the meaning attached to these values has changed.

Two circuits involving switches a, b.... are said to be equivalent if the closure conditions of the two circuits are the same for any given position of the switches involved (values of the variables a, b, ...).  That is, they are equivalent if for every position of the switches, current may either pass through both (both closed) or not pass through either  (both open). Two algebraic expressions are defined to be equal if and only if they represent equivalent circuits.

From these definitions, it should be clear that the only circuit properties of interest in the algebra of circuits are closure properties. That is, we will investigate only those factors which determine whether a circuit is open or closed, and will not be interested in problems concerning the resistance, amount of current or voltage, etc. It will be enough to know whether the circuit will carry a current, and we will ignore all quantitative considerations. This situation is an exact analogy of the situation in logic, where Boolean algebra was found capable of handling only that part of logic dependent on the truth values of propositions.  Shades of meaning, and all considerations other than truth values, are beyond the reach of algebraic techniques.

It is now possible, by drawing the appropriate circuits and enumerating the possible positions of the switches involved, to check that each of the laws of Boolean algebra is valid when interpreted in terms of switching

FIG. 1-2. Distributive law for (+) over (.).

TABLE 1-1

CLOSURE PROPERTIES OF SWITCHING FUNCTIONS a', ab, AND a+ b

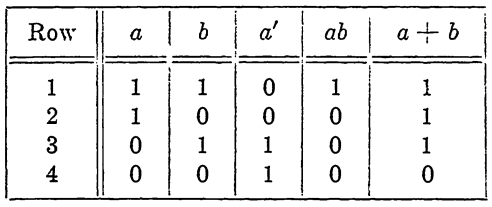
circuits. For example, consider the circuits that realize the functions on each side of the identity stating the distributive law for (+) over(.) shown in Fig. 1-2. By inspection, it is apparent that the circuit is closed  (current can pass) if switch .r is closed, or if both y and z are closed, and that the circuit is open (current cannot pass) if x and either y or z are open. Hence the circuits are equivalent, and this distributive law holds.  A simpler procedure for checking the validity of the fundamental laws is to note that numerical values of the switching functions a', ab, and a + b are identical to the truth tables for the corresponding propositional functions (Table 1-1). Hence the verification by truth tables of the postulates of Boolean algebra given in (SYMBOLIC LOGIC AND THE ALGEBRA OF PROPOSITIONS) is also a proof that the algebra of circuits is a Boolean algebra. The student should write out these proofs as a review.

EXAMPLE 1. Find a circuit which realizes the Boolean function xyz' +x'(y + z').

Solution. This expression indicates a series connection of .r, y, and z' in parallel with a circuit corresponding to x'(y + z'). This latter circuit consists of x' in series with a parallel connection of y and z'. Hence the circuit diagram is that shown in Fig. 1-3.

EXAMPLE 2. Find the Boolean function which represents the circuit shown in Fig. 1-4.

Solution. By inspection, the function is (x + y' + z)uv(yz' + x + y'u).

                                                  Fig. 1-3

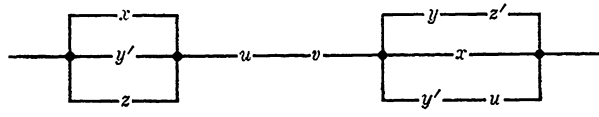
                                                Fig. 1-4

EXAMPLE 3. Construct the table of closure properties for the function f = x'y + z(x + y').

Solution. A table of closure properties for a function is identical, except for interpretation, to a truth table for a propositional function. This function has the closure properties listed in Table 1-2.

TABLE 1-2

CLOSURE PROPERTIES FOR THE FUNCTION f = x'y + z(x + y')