A formal presentation of Boolean algebra, which will be given in Chapter (BOOLEAN ALGEBRA), begins with a description of the symbols to be used and a statement of the axioms which it is assumed the symbols satisfy. Upon this foundation, a framework of theorems and definitions is constructed which becomes a mathematical model to be used in any application which the model seems to fit. The validity of the results obtained from the application depend upon the closeness with which themodel fits the practical situation.

In THE ALGEBRA OF SETS, however, a different approach to Boolean algebra has been adopted. An application has been considered first, with the hope that the reading will be more pleasant and to provide a strong motivation for the axiomatic treatment to follow. This approach has its weaknesses, of course.

The greatest is that we have no formal basis upon which to build precise proofs. Since there are no axioms to employ in writing proofs, we must rely upon an intuitive notion of the meanings of terms like "set" and "element." To strengthen this intuition and provide some justification for the basic laws which are valid in the algebra of sets, we shall introduce the concept of a Venn diagram. It should be remembered that such diagrams do not constitute proofs, but rather represent illustrations which make the laws seem plausible.

In a Venn diagram the set of points interior to a rectangle is taken as the universal set. Arbitrary sets within the universal set are represented by the sets of points interior to circles (or other closed regions) within the rectangle. If nothing specific is known about the sets involved, these circles are drawn so that all the possibilities of intersections among the sets are represented. By shading appropriate areas, all combinations of the sets can be represented graphically.

As an illustration of the usefulness of Venn diagrams, consider Fig. 1-1,  representing two sets X and Y which have a nonzero intersection. In this

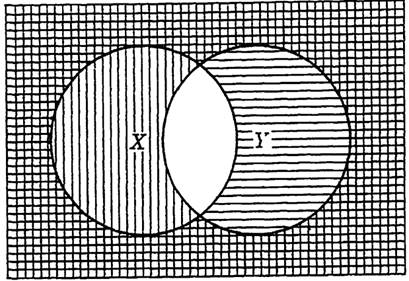
                                 FIG. 1-1. A Venn diagram involving sets X and Y.

figure X', the complement of set X, is shaded with horizontal lines, and Y' is shaded with vertical lines. The set X'Y' appears as the crosshatched area, which is clearly the complement of X + Y. Thus we have illustrated a basic law, that (X + Y)' = X'Y'. In the figure, the unshaded area represents X Y, which is clearly the complement of X' + Y', the area shaded either with horizontal lines, or vertical lines, or both. This illustrates a second basic law, namely, that (XY)' = X' + Y'.

As another illustration, consider Fig. 1-2, which illustrates the law X + YZ = (X + Y) (X + Z). This diagram is constructed in steps to show more clearly how the required sets are determined. The diagrams are self-explanatory.

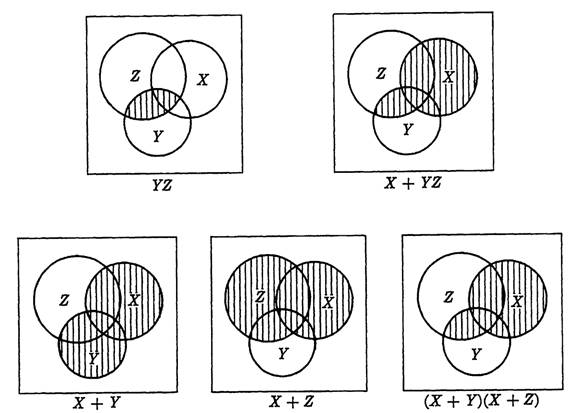
FIG. 1-2. Venn diagrams for the law X + YZ = (X + Y)(X + Z).

مواضيع ذات صلة

Zero Polynomial

Kronecker,s Polynomial Theorem

THE ALGEBRA OF SETS-The number of elements in a set

THE ALGEBRA OF SETS-Solution of equations

THE ALGEBRA OF SETS-Conditional equations

THE ALGEBRA OF SETS-Properties of set inclusion

THE ALGEBRA OF SETS- Expanding, factoring, and simplifying

THE ALGEBRA OF SETS-Fundamental laws

THE ALGEBRA OF SETS-The combination of sets

THE ALGEBRA OF SETS-Element and set

THE ALGEBRA OF SETS-Introduction

SYMBOLIC LOGIC AND THE ALGEBRA OF PROPOSITIONS-Special problems