
The Simple Pendulum
 المؤلف:
Professor John W. Norbury
المؤلف:
Professor John W. Norbury
 المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
 الجزء والصفحة:
p 183
الجزء والصفحة:
p 183
 30-12-2016
30-12-2016
 3924
3924
The Simple Pendulum
A pendulum is a very important type of oscillating motion and a very important clock (e.g. ''Grandfather Clock"). Let's analyze the forces and show that the period is independent of amplitude.
Example Prove that the period of a pendulum undergoing small oscillations is given by 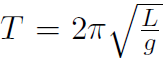 where L is the length of the pendulum.
where L is the length of the pendulum.
Solution we have
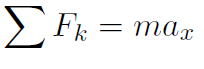
where we take the x direction to be perpendicular to the string. Thus
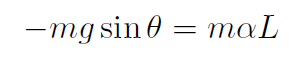
where α is the angular acceleration 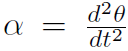 . Now for small oscillations, sin θ
. Now for small oscillations, sin θ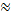 θ, so that
θ, so that
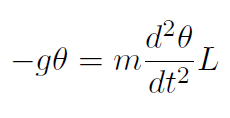
Now compare this to our spring equation which was
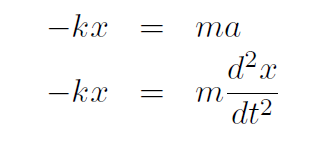
which had period 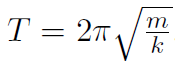 . Thus for the pendulum we must have
. Thus for the pendulum we must have
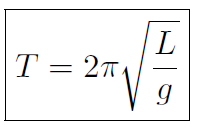
Example Prove that the period of oscillation is 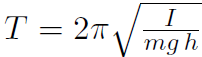 , where I is the rotational inertia, m is the total mass and h is the distance from the rotation axis to the center of mass. Assume small oscillations.
, where I is the rotational inertia, m is the total mass and h is the distance from the rotation axis to the center of mass. Assume small oscillations.
Solution The torque is
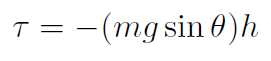
where the minus sign indicates that when θ increases the torque acts in the opposite direction. For small oscillations sin θ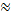 θ giving
θ giving
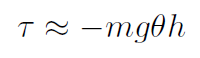
Substitute into Newton's second law
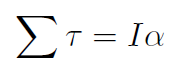
gives
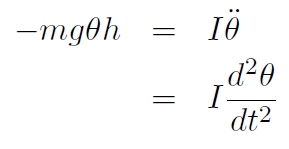
Now compare this to our spring equation which was
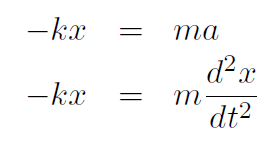
which had period 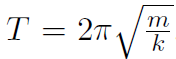 . Thus for the physical pendulum we must have
. Thus for the physical pendulum we must have
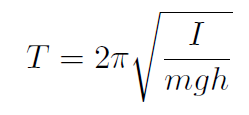
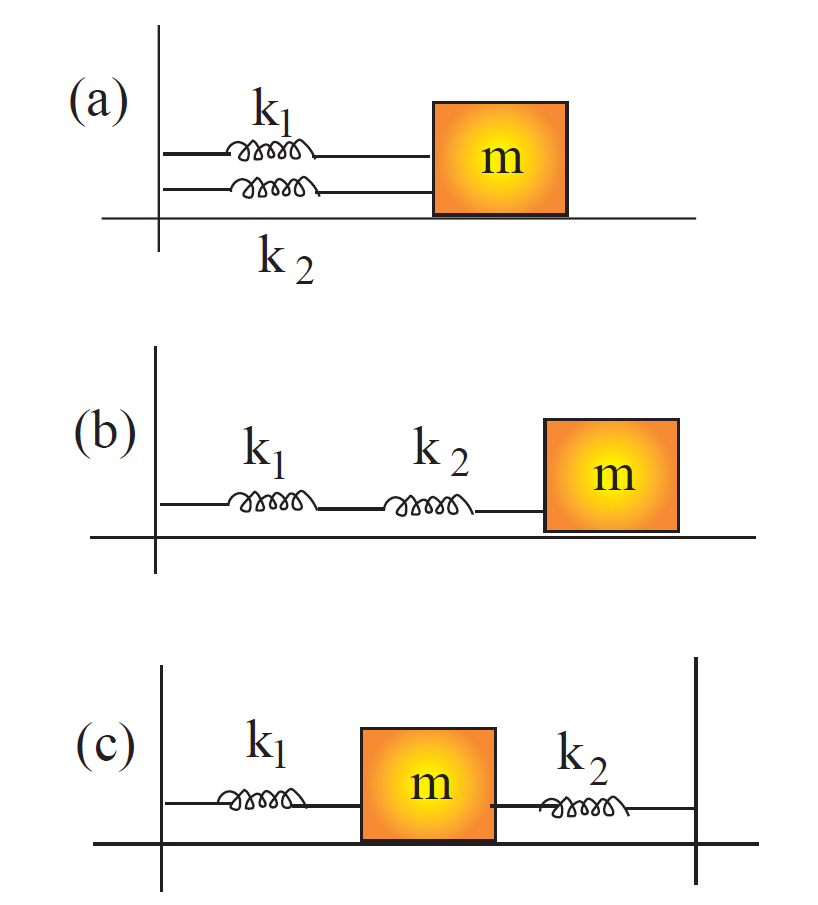
FIGURE 1.1 Block sliding on frictionless surface with various spring combinations.
Example Two springs, with spring constants k1 and k2, are connected in parallel to a mass m sliding on a frictionless surface, as shown in Fig. 1.1a. What is the effective spring constant K? (i.e. If the two springs were replaced by a single spring with constant K, what is K in terms of k1 and k2?) Assume both springs have zero mass.
Solution If m moves by an amount x then it feels two forces -k1x and -k2x, giving

giving
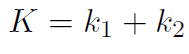
Example The two springs of the previous example are connected in series, as shown in Fig. 1.1b. What is the effective spring constant K ?
Solution If spring 1 moves a distance x1 and spring 2 moves a distance x2 then the mass moves a distance x1 + x2. The force the mass feels is

Now consider the motion of the mass plus spring 2 system. The force it feels is
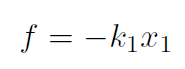
but we must have F = f because ma is same for mass m and mass plus spring 2 system because spring 2 has zero mass. Thus
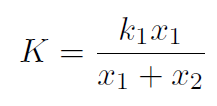
but
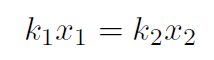
(the ratio of stretching 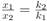 is inversely proportional to spring strength.) Thus
is inversely proportional to spring strength.) Thus 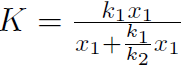 giving
giving
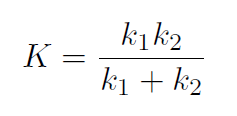
or
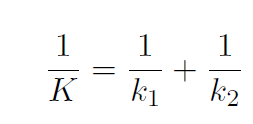
Example The two springs of the previous example are connected as shown in Fig.1.1c. What is the effective spring constant K ?
Solution If spring 1 is compressed by x then spring 2 is stretched by -x. Thus

giving
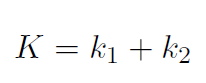
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


