
Keplers Laws
 المؤلف:
Professor John W. Norbury
المؤلف:
Professor John W. Norbury
 المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
 الجزء والصفحة:
p 170
الجزء والصفحة:
p 170
 29-12-2016
29-12-2016
 2852
2852
Kepler's Laws
Let's now use Newton's law of gravitation to prove some of Kepler's laws of planetary motion. Kepler's first law is that the planets move in elliptical orbits with the Sun at one focus. This is somewhat difficult to prove and we will leave it to a more advanced physics course. A picture is shown in Figure 1.1 with the Sun at the focus of an ellipse.

FIGURE 1.1 Planets sweep out equal areas in equal times.
Kepler's second law states that the line joining a planet to the Sun sweeps out equal areas in equal times. This is shown in Fig. 1.1. In the upper part of the figure there are two shaded regions with the same area. The planet takes the same time Δt to sweep out this area. Thus the planets move quickly when close to the Sun and move slowly when farther away.
Example Prove that Kepler's second law can be derived from Newton's law of universal gravitation.
Solution Figure 1.2 shows the radius vector  and the displacement
and the displacement 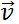 dt for the planet of mass m.
dt for the planet of mass m.
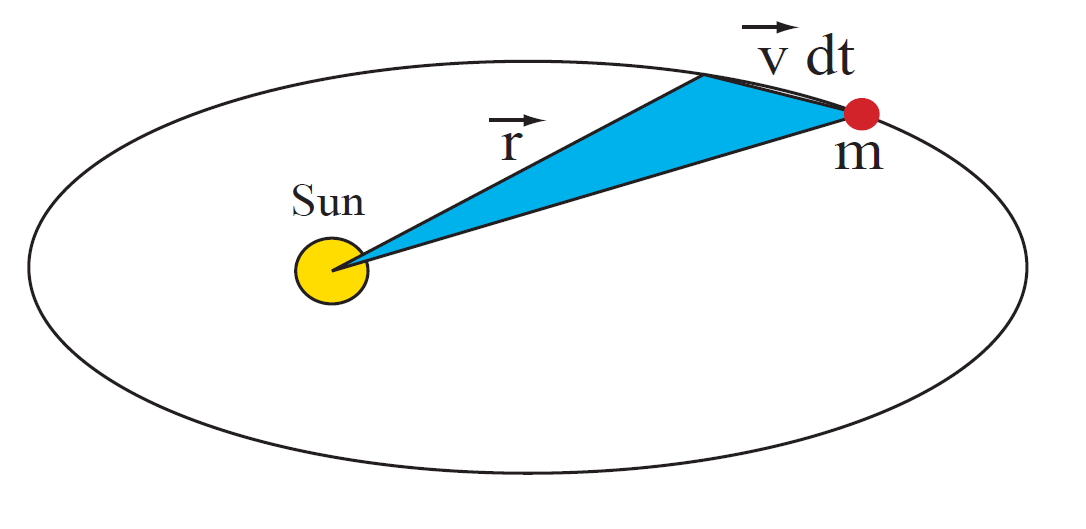
FIGURE 1.2 Area swept out by planet.
The shaded portion is the area swept out and has the shape of a triangle of area
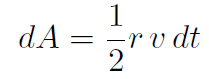
The rate of change of area is

where l is the angular momentum of the planet. But angular momentum is constant, therefore
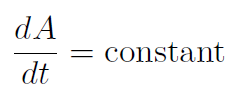
meaning that equal areas are swept out in equal times!
Kepler's third law is that the period squared is proportional to the average distance cubed (T2 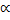 r3) for a planetary orbit. This is difficult to prove for elliptical orbits, which is done in a more advanced physics course. We will prove it for a circular orbit only. Actually the essenticity of the elliptical orbits are typically very small. In other words the elliptical orbits are very close to circular orbits with the Sun at the center. We shall prove Kepler's other two laws with the assumption that the orbits are circles. Thus we immediately know that the right hand side of F = ma is
r3) for a planetary orbit. This is difficult to prove for elliptical orbits, which is done in a more advanced physics course. We will prove it for a circular orbit only. Actually the essenticity of the elliptical orbits are typically very small. In other words the elliptical orbits are very close to circular orbits with the Sun at the center. We shall prove Kepler's other two laws with the assumption that the orbits are circles. Thus we immediately know that the right hand side of F = ma is  because all uniform circular motion has the centripetal acceleration given by
because all uniform circular motion has the centripetal acceleration given by 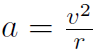 .
.
Example Prove that Kepler's third law can be derived from Newton's law of universal gravitation. (Assume circular orbits only)
Solution F = ma
gives
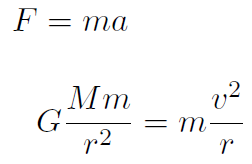
Now the period T is the time to complete one orbit. Thus
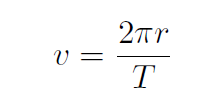
or

giving

or
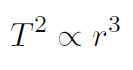
Example The distance between Earth and the Sun is about 93 million miles and can easily be determined using parallax and trigonometry. How can the mass of the Sun be subsequently determined?
Solution Kepler's law is  giving
giving
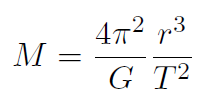
Now r = 93,000,000 miles = 150,000,000 km and the period of Earth is 1 year or
T = 365 × 24 × 60 × 60 sec
Thus the mass of the Sun is
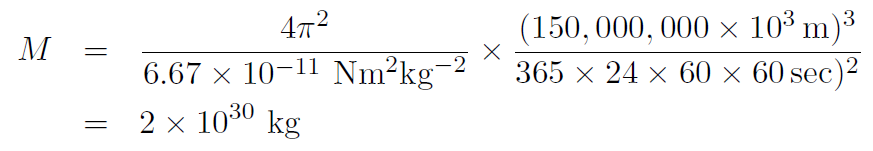
Notice that the mass of Earth did not enter. Thus if we observe two bodies in orbit and know the distance between them we can get the mass of the other body. this is how astronomers determine the mass of double star systems. (More than half of the stars in the sky are actually double stars.)
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


