
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The Center of Mass
المؤلف:
Professor John W. Norbury
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
الجزء والصفحة:
p 108
28-12-2016
3180
The Center of Mass
Systems of Particles
Now let's come up with a mathematical definition for center of mass which is more precise than just saying it's the balance point (although the balance point always gives the correct answer). The location of the center of mass is defined as
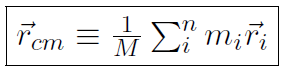 (1.1)
(1.1)
where the sum over i running from 1 to n means sum over all of the point particles within the body, assuming there are a total of n point particles. M is the total mass of all the individual bodies and can be written
 (1.2)
(1.2)
We have defined the center of mass. Now let's see if our definition makes sense. First of all it's a vector equation and so what it really means is the usual 3-dimensional decomposition as
 (1.3)
(1.3)
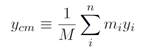 (1.4)
(1.4)
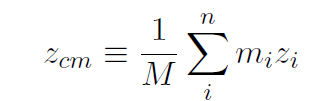 (1.5)
(1.5)
Let's just consider the 1-dimensional version for the case of 2 bodies only. Then the total mass M becomes
 (1.6)
(1.6)
and (1.2) becomes
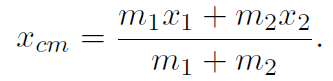 (7.7)
(7.7)
Does this make sense ? Let's see.
Example Where is the position of the center of mass for a system consisting of two dumbells, each with the same mass m each at the end of a 4ft massless rod ?
Solution Now you know that the answer to this must be at the center of the rod. After all that is the balancing point. That is our guess is that xcm = 2ft. Let's use our definition of center of mass, equation (1.1) and see if it gives this answer. Now we have a 1-dimensional problem and therefore (1.1) reduces to only (1.3). Furthermore we only have two bodies and this reduces further to (1.7). Choosing the origin of the x-coordinate system to be at the left dumbell gives x1 = 0ft and x2 = 4ft. Substituting gives
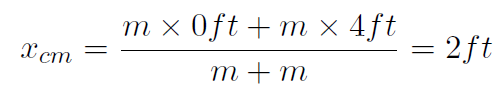 (1.8)
(1.8)
which is exactly what we expected. Therefore we can believe that our definition for center of mass (1.1) makes perfect sense. Let's look at what happens if we use a different coordinate system.
Example Repeat the previous problem, but with the x-origin located at the center between the two dumbells instead of on the left dumbell.
Solution Well now we would guess that the center of mass would be given by xcm = 0. Let's see if our formula works here. With the origin of the x-axis chosen to be at the center of the dumbells we have the position of each dumbell given by x1 = -2ft and x2 = +2ft respectively. Subsituting we get
 (1.9)
(1.9)
which is exactly what we expected. Therefore again we can believe that our definition for center of mass (1.1) makes perfect sense. Being able to find the center of mass is actually useful, as the following example shows.
Example A baby of mass mB sits on a see-saw. Mary's mass is mM. Where should Mary sit in order to balance the see-saw ? Work out a formula and also a numerical answer if mB = 10 kg and mM = 80 kg.
Solution Again our intuition tells us that we can guess that the ratio of the distances should be 1/8. That is the baby should be 8 times as far away from the center of the see-saw as Mary. Let's see if our center of mass definition (1.1) tells us this. Again this is a 1-dimensional, 2-body problem and so the formula for the center of mass is again
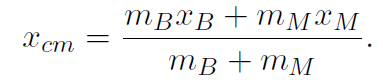
Now we want the center of mass located at the center of the see-saw and we will put the origin of our x-axis there as well.
Thus
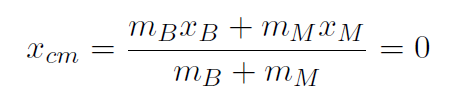
giving

which means that
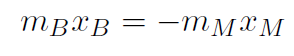
or
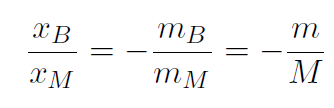
or

Putting in numbers we get
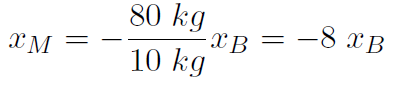
just as we suspected.
Rigid Bodies
Above we considered finding the center of mass of two bodies. This can easily be extended to 3 or more bodies and some of this will be explored in the homework. That's all well and good, but how do we find the center of mass of systems made up of millions of particles such as a baseball bat. In other words how do we find the center of mass of rigid bodies ? That's what we will look at now. In physics whenever we want to change our study from a collection of discrete particles (desribed by a sum Σi) to a continuous collection of particles, the sum just changes to an integral. Hopefully this makes perfect sense from what you have studied in calculus. You all now know that an integral is just the limit of a sequence of sums. Now each of the millions of particles in a rigid body has a tiny little mass denoted by dm. For a discrete collection of particles we had (1.1) as
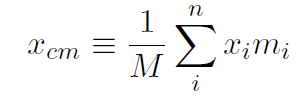 (1.10)
(1.10)
but for a continuous distribution of particles we now define
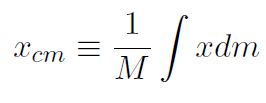 (1.11)
(1.11)
This is easier to work with if we introduce density 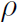 as mass / volume or
as mass / volume or
 (1.12)
(1.12)
where dV is the volume occupied by the mass dm. Thus our definition can be written
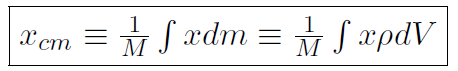
and the same for y and z. If the density is constant, then it can be taken outside the integral to give
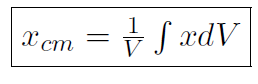
and the same for y and z. There's one additional catch. Above we defined a 3-dimensional density as mass / volume. But what if we have a dense 1-dimensional object such as a very long and thin pencil. Well then we will want a linear mass density. Instead of  , we use the symbol ¸ for linear mass density and define it as
, we use the symbol ¸ for linear mass density and define it as

so that now we have
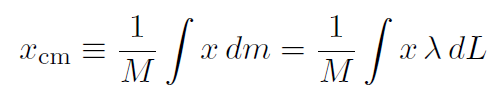
and for a constant λ,

Because this is linear mass density we do not have any equations for x or y. Similarly we may have mass distributed only in 2 dimensions such as the surface of a table. We use area mass density defined as
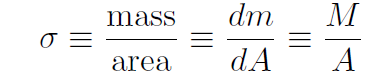
giving
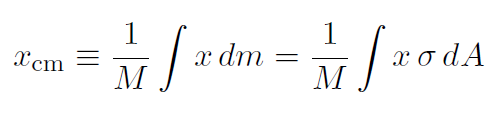
and for constant σ,

and similarly for y; but there is no equation for z. (why?)
Example Locate the center of mass of a very thin pencil of length L balanced sideways.
Solution Again using intuition we know the answer must be at the center of the pencil. Now the element of length dL ≡ dx, and the linear mass density ¸ of the pencil is constant, so that
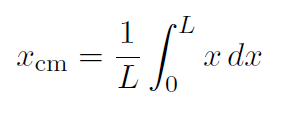
We have taken the origin (x = 0) to be at one end of the pencil.
Thus
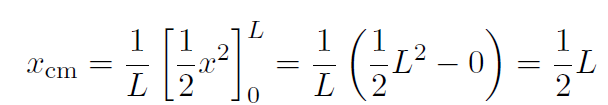
which is just the answer we expected! Thus we can believe that the formulas given previously really do work
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















