

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Differentiation and Integration in RN-The Derivative in RN
المؤلف:
Murray H. Protter
المصدر:
Basic Elements of Real Analysis
الجزء والصفحة:
136-140
24-11-2016
1252
Each partial derivative of a function f : RN → R1 isa mapping from RN into R1. This generalization of the ordinary derivative, useful for many purposes, singles out a particular direction in which the differentiation is performed. We now take up another extension of the ordinary derivative, one in which the difference quotient tends to a limit as x → a regardless of the direction of approach.
Let A be an open subset of RN, and suppose that f and g are functions from A into R1. We denote by d(x, y) the Euclidean distance between two points x, y in RN.
Definition
The continuous functions f and g are tangent at a point a ∈ A if
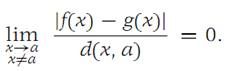
We note that if two functions are tangent at a point a, then necessarily f(a) = g(a). Also, if f , g, and h are functions with f and g tangent at a and with g and h tangent at a, then we verify simply that f and h are tangent at a. To see this, observe that
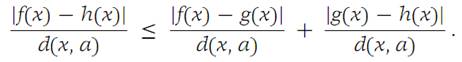
As x → a, the right side tends to 0, and so must the left side.
Let L : RN → R1 be a linear function; that is, L is of the form
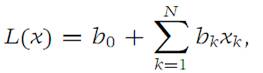
where b0,b1,...,bN are real numbers. It may happen that a function f is tangent to a linear function at a point a. If so, this linear function is unique, as we now show.
Theorem 1.1
Suppose that L1 and L2 are linear functions tangent to a function f at a point a. Then L1 ≡ L2.
Proof
It is convenient to write the linear functions L1 and L2 in the form
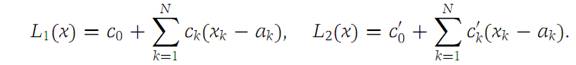
From the discussion above, it follows that L1(a) = L2(a) = f(a). Hence, c0 = c/0. Also, for every Ԑ> 0, we have(1.1)
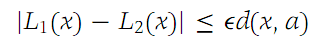
for all x sufficiently close to a. For z ∈ RN, we use the notation z=d(z, 0). Now, with δ a real number, choose
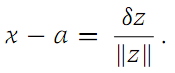
Then, for sufficiently small |δ|, we find from inequality (1.1) that
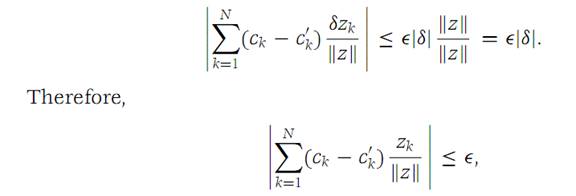
and since this inequality holds for all positive Ԑ, we must have ck = c/k, k =1, 2,...,N.
Definitions
Suppose that f : A → R1 is given ,where A is an open set in RN containing the point a. The function f is differentiable at a if there is a linear function
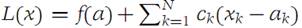
that is tangent to f at a. A function f is differentiable on a set A in RN if it is differentiable at each point of A. The function L is called the derivative, or total derivative, of at . We use the symbol f/(a) for the derivative of f at the point a in RN.
Theorem 1.2
If f is differentiable at a point a, then f is continuous at a. The proof is left to the reader. (Problem3 at the end of this section.) As we saw in Section of (Partial Derivatives and the Chain Rule (, a function f may have partial derivatives without being continuous. suggests that differentiability is a stronger condition than the existence of partial derivatives. The next theorem verifies this point.
Theorem 1.3
If f is differentiable at a point a, then all first partial derivatives of f exist at a.
Proof
Let L be the total derivative of f at a. We write
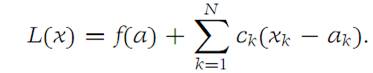
From the definition of derivative, it follows that(1.2)
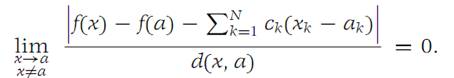
For x we choose the element a + h, where h = (0, 0,..., 0,hi , 0,..., 0). Then equation (1.2) becomes
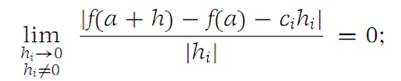
we may therefore write(1.3)

where Ԑ(hi) → 0as hi → 0.
We recognize the left side of equation (1.3) as the expression used in the definition of f,i(a). In fact, we conclude that
ci =f,i(a), i = 1, 2,...,N.
A partial converse of Theorem1.3 is also true.
Theorem 1.4
Suppose that f,i , i = 1,2,...,N, are continuous at a point a. Then f is differentiable at a. This result is most easily established by means of the Taylor expansion with remainder with n= 0. We leave the details for the reader.
Definitions
Suppose that f possesses all first partial derivatives at a point a in RN. The gradient of f is the element in RN whose components are (f,1(a), f,2(a),...,f,N(a)). We denote the gradient of f by ∇f or grad f .
Suppose that A is a subset of RN and f : A → R1 is differentiable on A. Let h =(h1,h2,...,hN) be an element of RN. We define the total differential df as that function from A × RN → R1 given by the formula(1.4)
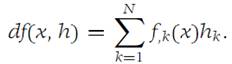
Using the inner or dot product notation for elements in RN, we may also write
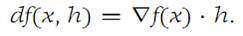
Equation (1.4) shows that the total differential (also called the dif ferential) of a function f is linear in h. The differential vanishes when x =a and h= 0. The Chain rule takes a natural form for differentiable functions, as the following theorem shows.
Theorem 1.5 (Chain rule)
Suppose that each of the functions g1,g2,...,gN is a mapping from RM into R1 and that each gi is differentiable at a point b= (b1,b2,...,bM). Suppose that f :RN → R1 is differentiable at the point a = (g1(b),g2(b),...,gN(b)).
Form the function

Then H is differentiable at b and
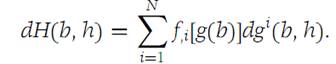
Problems
1. Let f and g be functions from RN into R1. Show that if f and g are differentiable at a point a, then f + g is differentiable at a. Also, αf is differentiable at a for every real number α.
2. Let f : R3 → R1 be given by
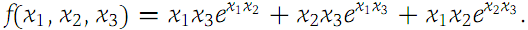
Find ∇f and df(x, h).
3. Suppose that all first partial derivatives of a function f : RN → R1 are continuous at a point a. Show that f is differentiable at a.(Theorem 1.4.)
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(136-140)
 الاكثر قراءة في التحليل الحقيقي
الاكثر قراءة في التحليل الحقيقي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















