


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | Basic Properties of Functions on R1 - The Intermediate-Value Theorem |
|
|
|
Read More
Date: 1-12-2016
Date: 30-11-2016
Date: 30-11-2016
|
The proofs of many theorems of calculus require a knowledge of the basic properties of continuous functions. In this section we establish the Intermediate-value theorem, an essential tool used in the proofs of the Fundamental theorem of calculus and the Mean-value theorem.
Theorem 1.1 (Nested intervals theorem)
Suppose that
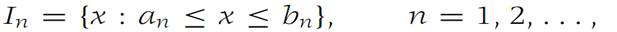
is a sequence of closed intervals such that In+1 ⊂ In for each n .If limn→∞ (bn−an) = 0, then there is one and only one number x0 that is in every In.
By hypothesis, we have an ≤ an+1 and bn ≤ bn+1. Since an <bn for every n, the sequence {an} is nondecreasing and bounded from above by b1 (see Figure 1.1). Similarly, the sequence bn is nonincreasing and bounded from below by a1. Using Axiom C, we conclude that there are
numbers x0 and x/ 0 such that an → x0, an ≤ x0, and bn → x/ 0, bn ≥ x/ 0,as n →∞. Using the fact that bn − an → 0, n →∞, we find that x0 = x/0and
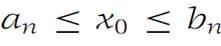
for every n. Thus x0 is in every In.

Figure 1.1 Nested intervals.
The hypothesis that each In is closed is essential. The sequence of half-open intervals
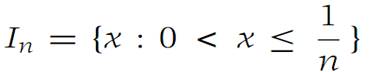
Has the property that In+1 ⊂ In for every n. Since no In contains0, any number x0 in all the In must be positive. But then by choosing N> 1/x0, we see that x0 cannot belong to IN ={x :0 <x ≤ 1/N}. Although the intervals In are nested, they have no point in common.
Before proving the main theorem, we prove the following result, which we shall use often in this chapter.
Theorem 1.2
Suppose f is continuous on [a,b], xn ∈ [a,b] for each n, and xn → x0. Then x0 ∈ [a,b] and f(xn) → f(x0).
Since xn ≥ a for each n, it follows from the theorem on the limit of inequalities for sequences that x0 ≥ a. Similarly, x0 ≤ b so x0 ∈ [a, b].
If a<x0 <b, then f(xn) → f(x0) on account of the composite function theorem (Theorem (Limit of a composite function) Suppose that f and g are functions on R1 to R1. Define the composite function h(x) = f [g(x)].If f is continuous at L and if g(x) → L as x → a, then,
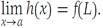 )
)
The same conclusion holds if x0 = a or b. A detailed proof of the last sentence is left to the reader.
We now establish the main theorem of this section.
Theorem 1.3 (Intermediate-value theorem)
Suppose f is continuous on [a,b], c ∈ R1, f(a)<c, and f(b)>c. Then there is at least one number x0 on [a,b] such that f(x0) =c.
Note that there may be more than one such x0, as indicated in Figure 1.2.
Define a1 = a and b1 = b. Then observe that f((a1 +b1)/2) is either equal to c, greater than c, or less than c. If it equals c, choose x0 = (a1 + b1)/2 and the result is proved. If f((a1 + b1)/2)>c, then define a2 = a1 and b2 =(a1 + b1)/2. If f((a1 + b1)/2)<c, then define a2 = ((a1 + b1)/2)and b2 b1.
In each of the last two cases we have f(a2)<c and f(b2)>c. Again compute f((a2 + b2)/2). If this value equals c, the result is proved. If
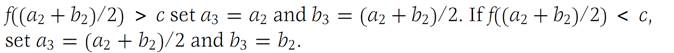

Figure 1.2 Illustrating the Intermediate-value theorem.
Continuing in this way, either we find a solution in a finite number of steps or we find a sequence {[an,bn]} of closed intervals each of which is one of the two halves of the preceding one, and for which we have(1.1)
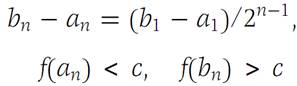
for each n.
From the Nested intervals theorem it follows that there is a unique point x in all these intervals and that

From Theorem 1.2, we conclude that
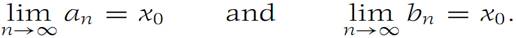
From inequalities(1.1) and the limit of inequalities it follows that f(x0) ≤ c
and f(x0) ≥ c, so that f(x0) = c.
Problems
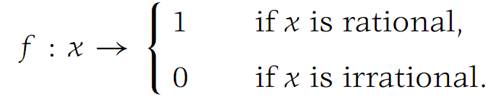
(a) Show that f is not continuous at any x0.
(b) Let g be a function with domain all of R1.If g(x)= 1if x is rational and if g is continuous for all x, show that g(x) = 1forx ∈ R1.
2. Prove the last sentence of Theorem 1.2.
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(42-44)



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
وفد العتبة الكاظمية المقدسة يزور عائلة الشهيد البطل النقيب حارث السوداني
|
|
|