


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-6-2021
Date: 6-7-2017
Date: 23-7-2021
|
We now show that, if a topological space X is the union of a finite collection of closed sets, and if a function from X to some topological space is continuous on each of these closed sets, then that function is continuous on X.
Lemma 1.1 Let X and Y be topological spaces, let f: X → Y be a function from X to Y , and let X = A1∪A2∪· · ·∪Ak, where A1, A2, . . . , Ak are closed sets in X. Suppose that the restriction of f to the closed set Ai is continuous for i = 1, 2, . . . , k. Then f: X → Y is continuous.
Proof A function f: X → Y is continuous if and only if f−1 (G) is closed in X for every closed set G in Y (Lemma 1.6). Let G be an closed set in Y . Then f−1 (G) ∩ Aiis relatively closed in Ai for i = 1, 2, . . . , k, since the restriction of f to Ai is continuous for each i. But Ai is closed in X, and therefore a subset of Ai is relatively closed in Ai if and only if it is closed in X. Therefore f−1 (G) ∩ Aiis closed in X for i = 1, 2, . . . , k. Now f−1 (G) isthe union of the sets f−1 (G) ∩ Ai for i = 1, 2, . . . , k. It follows that f−1 (G), being a finite union of closed sets, is itself closed in X. It now follows from Lemma that f: X → Y is continuous.
Example: Let Y be a topological space, and let α: [0, 1] → Y and β: [0, 1] → Y be continuous functions defined on the interval [0, 1], where α(1) = β(0).
Let γ: [0, 1] → Y be defined by
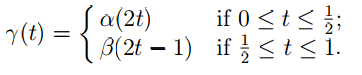
Now γ|[0, 1/2] = α ◦ ρ where ρ: [0, 1/2] → [0, 1] is the continuous function defined by ρ(t) = 2t for all t ∈ [0, 1/2]. Thus γ|[0, 1/2] is continuous, being a composition of two continuous functions. Similarly γ [1/2, 1] is continuous. The subintervals [0, 1/2 ] and [1/2 , 1] are closed in [0,1], and [0,1] is the union of these two subintervals. It follows from Lemma 1.1 that γ: [0; 1] ! Y is continuous.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|