


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 14-8-2016
Date: 25-7-2016
Date: 9-8-2016
|
Principle of Conformal Mapping
a) Show that the real part U(x, y) and the imaginary part V(x, y) of a differentiable function W(z) of z = z + iy obey Laplace’s equation.
b) If U(x, y) and V(x, y) above are the potentials of two fields F and G in two dimensions, show that at each point (x, y), the fields F and G are orthogonal.
c) Consider the function W(z) = A ln z, where A is a real constant. Find the fields F and G and mention physical (Electrodynamics) problems in which they might occur.
SOLUTION
A differentiable function W(z) = U(x, y) + iV (x, y) satisfies the Cauchy Riemann conditions
 (1)
(1)
To check that U and V satisfy Laplace’s equation, differentiate (1)
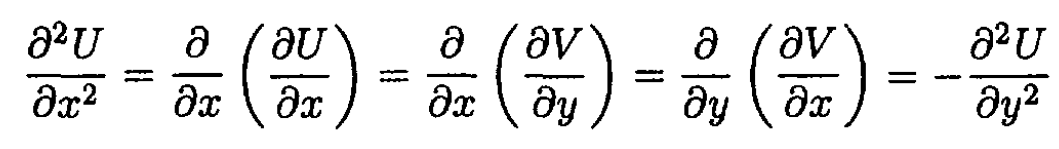
or

Similarly,
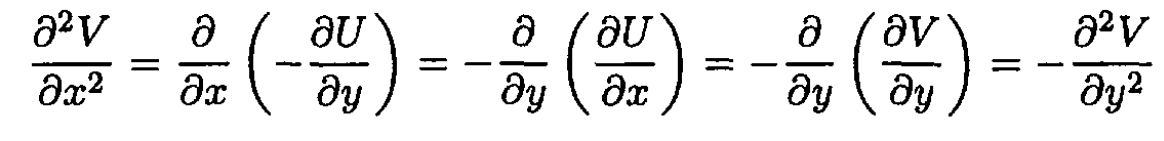
and
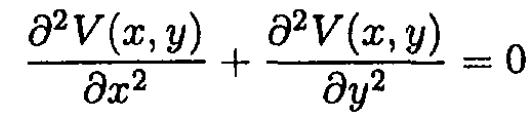
b) Orthogonality of the functions F and G also follows from (1):
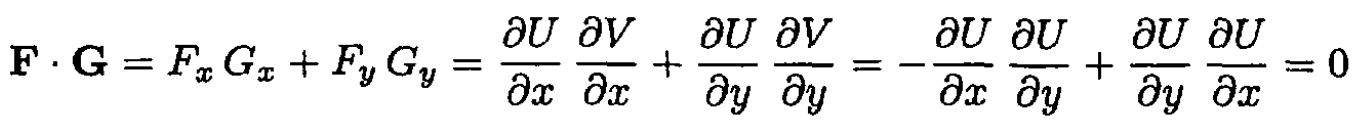
c) The electric field of an infinitely long charged wire passing through the origin is given by 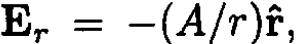 where A = -2λ and λ is the charge per unit length, r is the distance from the wire (see Figure 1.1). The complex potential
where A = -2λ and λ is the charge per unit length, r is the distance from the wire (see Figure 1.1). The complex potential
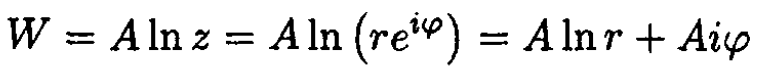
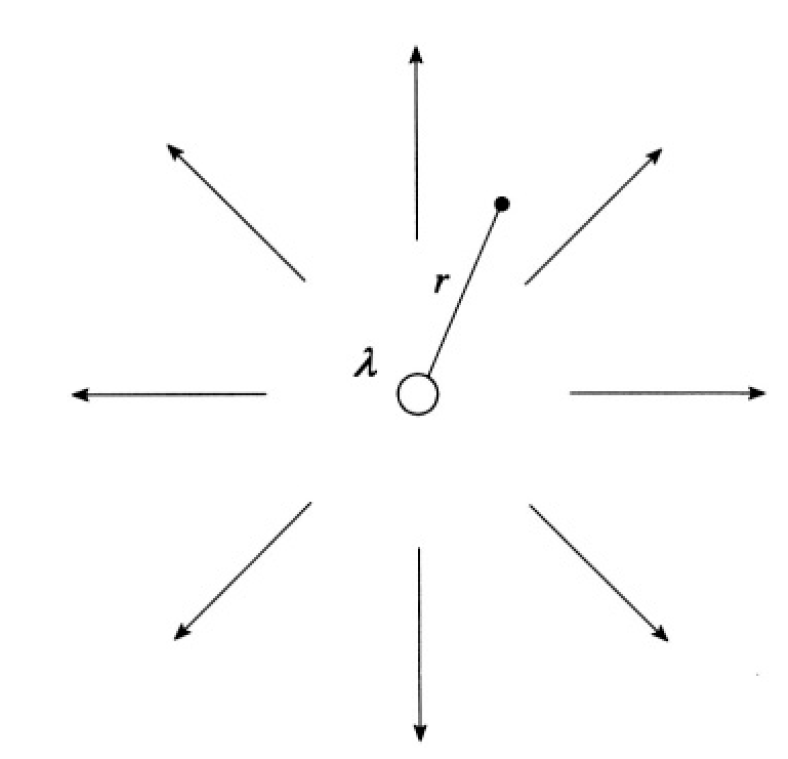
Figure 1.1
So
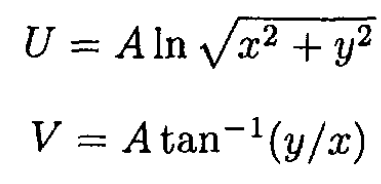
The fields F and G are given by
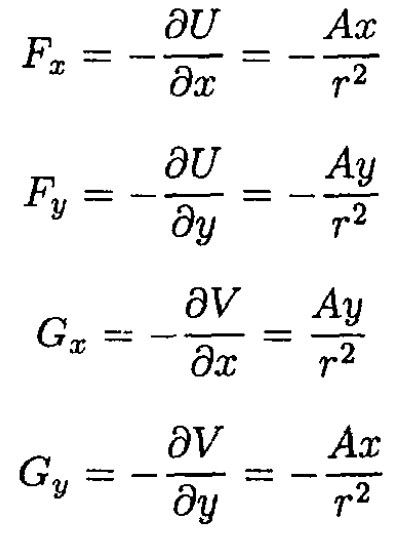
Note how F and G satisfy the conditions of parts (a) and (b). The magnetic field of a similarly infinite line current can be described by the same potential.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
عوائل الشهداء: العتبة العباسية المقدسة سبّاقة في استذكار شهداء العراق عبر فعالياتها وأنشطتها المختلفة
|
|
|