


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-7-2016
Date: 11-5-2022
Date: 19-3-2022
|
In this section we consider several classic results concerning matchings. We begin with a few more definitions. Given a graph G and Amatching M ,an M-alternating path is a path in G where the edges alternate between M-edges and non-M-edges .An M-augmenting path is an M-alternating path where both end vertices are M-unsaturated. As an example, consider the graph G and the matching M indicated in Figure 1.1.
An example of an M-alternating path is c, a, d, e, i. An example of an M-augmenting path is j, g, f, a, c, b. The reason for calling such a path “Maugmenting” will become apparent soon.
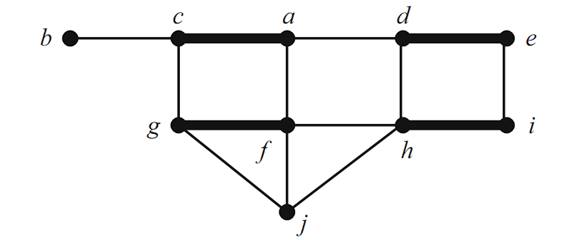
FIGURE 1.1. The graph G and matching M.
The following result is due to Berge [2].
Theorem 1.1 (Berge’s Theorem).
Let M be a matching in a graph G. M is maximum if and only if G contains no M-augmenting paths.
Proof. First, assume that M is a maximum matching, and suppose that P :
v1,v2,...,vk is an M-augmenting path. Due to the alternating nature of M-augmenting paths, it must be that k is even and that the edges v2v3, v4v5, ... , vk−2vk−1 are all edges of M. We also see that the edges v1v2, v3v4, ... , vk−1 vk are not edges of M (Figure 1.2).
But then if we define the set of edgesM1 to be

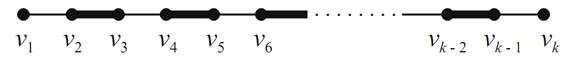
FIGURE 1.2. An M-augmenting path.
then M1 is a matching that contains one more edge than M, a matching that we assumed to be maximum. This is a contradiction, and we can conclude that G contains no M-augmenting paths.
For the converse, assume that G has noM-augmenting paths, and suppose that M/is a matching that is larger than M. Define a subgraph H of G as follows: Let V (H)= V (G) and let E(H) be the set of edges of G that appear in exactly one of M and M/. Now consider some properties of this subgraph H. Since each of the vertices of G lies on at most one edge from M and at most one edge from M/, it must be that the degree (in H) of each vertex of H is at most 2. This implies that each connected component of H is either a single vertex, a path, or a cycle. If a component is a cycle, then it must be an even cycle, since the edges alternate between M-edges and M/-edges. So, since |M/| > |M|, there must be at least one component of H that is a path that begins and ends with edges from M/.
But this path is an M-augmenting path, contradicting our assumption. Therefore, no such matching M/ can exist—implying that M is maximum.
Before we see Hall’s classic matching theorem, we need to define one more term. If G is a bipartite graph with partite sets X and Y , we say that X can be matched into Y if there exists a matching in G that saturates the vertices of X. Consider the two examples in Figure 1.3. In the bipartite graph on the left,
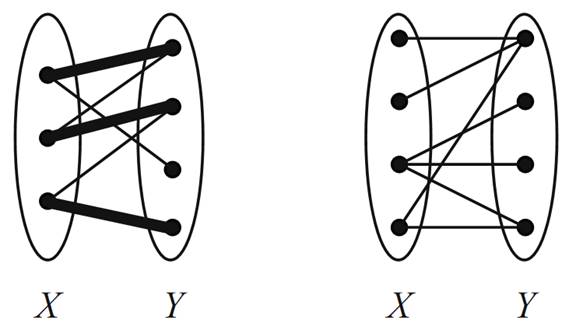
FIGURE 1.3.
we see that X can be matched into Y . In the graph on the right, though, it is impossible to match X into Y. What conditions on a bipartite graph must exist if we want to match one partite set into the other? The answer to this question is found in the following result of Hall [3] (Philip, not Monty).
Recall that the neighborhood of a set of vertices S, denoted by N(S),is the union of the neighborhoods of the vertices of S.
Theorem 1.2 (Hall’s Theorem).
Let G be a bipartite graph with partite sets X and Y . X can be matched into Y if and only if |N(S)|≥|S| for all subsets S of X.
Proof. First suppose that X can be matched into Y ,and let S be some subset of X. Since S itself is also matched into Y , we see immediately that |S|≤|N(S)|
(see Figure 1.4). Now suppose that |N(S)|≥|S| for all subsets S of X, and
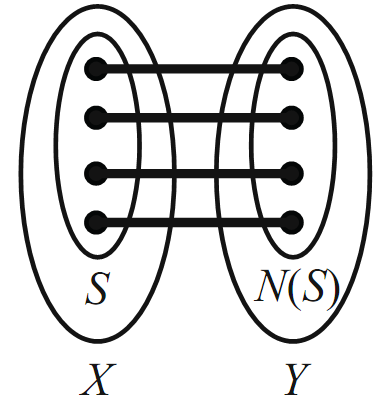
FIGURE 1.4.
let M be a maximum matching. Suppose that u ∈ X is not saturated by M (see Figure 1.5).Define the set A to be the set of vertices of G that can be joined to u
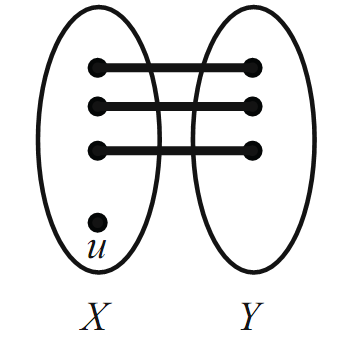
FIGURE 1.5.
by an M-alternating path. Let S = A∩X, and let T = A∩Y (see Figure 1.6). Notice now that Berge’s Theorem implies that every vertex of T is saturated by
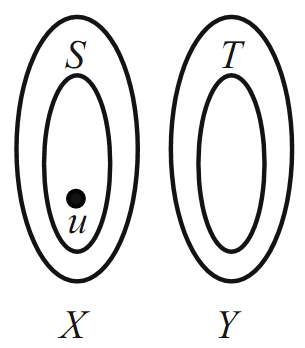
FIGURE 1.6.
M and that u is the only unsaturated vertex of S. That is, every vertex of T is saturated, and every vertex of S {u} is saturated. This implies that |T | = |S|−1.
It follows from Berge’s Theorem and the definition of T that N(S)= T . But then we have that |N(S)| = |S|− 1 < |S|, and this is a contradiction. We conclude that such a vertex u cannot exist in X and that M saturates all of X.
Given some family of sets X,a system of distinct representatives, or SDR ,for the sets in X can be thought of as a “representative” collection of distinct elements from the sets of X. For instance, let S1, S2, S3, S4,and S5 be defined as follows:
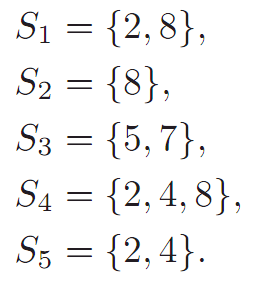
The family X1 = {S1,S2,S3,S4} does have an SDR, namely {2, 8, 7, 4}.The family X2 = {S1,S2,S4,S5} does not have an SDR.
So under what conditions will a finite family of sets have an SDR? We answer this question with the following theorem.
Theorem 1.3.
Let S1, S2, ..., Sk be a collection of finite, nonempty sets. This collection has an SDR if and only if for every t ∈{1,...,k}, the union of any t of these sets contains at least t elements.
Proof. Since each of the sets is finite, then of course S = S1 ∪ S2 ∪···∪ Sk is finite. Let us say that the elements of S are a1, ..., an.
We now construct a bipartite graph with partite sets X = {S1,...,Sk} and Y = {a1,...,an} (Figure 1.7). We place an edge between Si and aj if and only if aj ∈ Si.
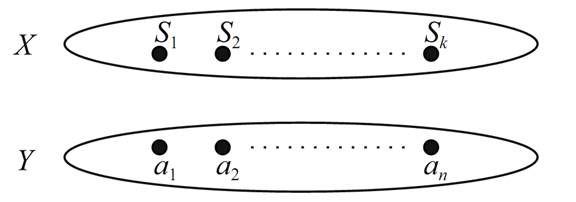
FIGURE 1.7. Constructing a bipartite graph.
Hall’s Theorem now implies that X can be matched into Y if and only if |A|≤|N(A)| for all subsets A of X. In other words, the collection of sets has an SDR if and only if for every t ∈{1,...,k}, the union of any t of these sets contains at least t elements.
________________________________________________________________________________
1-Combinatorics and Graph Theory, Second Edition, John M. Harris • Jeffry L. Hirst • Michael J. Mossinghoff,2000,page(104-108)
2-C. Berge, Two theorems in graph theory, Proc. Natl. Acad. Sci. USA 43 (1957), 842–844.
3-P. Hall, On representation of subsets, J. London Math. Soc. 10 (1935), 26–30.
4- J. Clark and D. A. Holton, A First Look at Graph Theory, World Scientific, Teaneck, NJ, 1991.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|