تاريخ الفيزياء
علماء الفيزياء
الفيزياء الكلاسيكية
الميكانيك
الديناميكا الحرارية
الكهربائية والمغناطيسية
الكهربائية
المغناطيسية
الكهرومغناطيسية
علم البصريات
تاريخ علم البصريات
الضوء
مواضيع عامة في علم البصريات
الصوت
الفيزياء الحديثة
النظرية النسبية
النظرية النسبية الخاصة
النظرية النسبية العامة
مواضيع عامة في النظرية النسبية
ميكانيكا الكم
الفيزياء الذرية
الفيزياء الجزيئية
الفيزياء النووية
مواضيع عامة في الفيزياء النووية
النشاط الاشعاعي
فيزياء الحالة الصلبة
الموصلات
أشباه الموصلات
العوازل
مواضيع عامة في الفيزياء الصلبة
فيزياء الجوامد
الليزر
أنواع الليزر
بعض تطبيقات الليزر
مواضيع عامة في الليزر
علم الفلك
تاريخ وعلماء علم الفلك
الثقوب السوداء
المجموعة الشمسية
الشمس
كوكب عطارد
كوكب الزهرة
كوكب الأرض
كوكب المريخ
كوكب المشتري
كوكب زحل
كوكب أورانوس
كوكب نبتون
كوكب بلوتو
القمر
كواكب ومواضيع اخرى
مواضيع عامة في علم الفلك
النجوم
البلازما
الألكترونيات
خواص المادة
الطاقة البديلة
الطاقة الشمسية
مواضيع عامة في الطاقة البديلة
المد والجزر
فيزياء الجسيمات
الفيزياء والعلوم الأخرى
الفيزياء الكيميائية
الفيزياء الرياضية
الفيزياء الحيوية
الفيزياء العامة
مواضيع عامة في الفيزياء
تجارب فيزيائية
مصطلحات وتعاريف فيزيائية
وحدات القياس الفيزيائية
طرائف الفيزياء
مواضيع اخرى
تحويل الدوائر الكهربائية التي على شكل Δ الى دوائر كهربائية على شكلY وبالعكس
المؤلف:
وفاء السواح
المصدر:
أساسيات الكهربائية التيارية
الجزء والصفحة:
...
14-7-2016
2349
+
-
20
تحويل الدوائر الكهربائية التي على شكل Δ الى دوائر كهربائية على شكلY وبالعكس
عند تطبيق قوانين كيرشوف لحل الدوائر الكهربائية تقابلنا صعوبات كبيرة و ذلك لوجود عدد كبير من المعادلات الآنية التي يجب حلها. و لسهولة حل مثل هذه الدوائر فانه يمكننا تحويل الدوائر الكهربائية التي على شكل Δ الى دوائر كهربائية على شكل Y و العكس.
أولا: تحويل →Y Δ
نفرض لدينا ثلاث مقاومات R12 , R23 , R31 متصلة على شكل Δ بين الأطراف1, 2 , 3 كما هو موضح بالشكل (a). المقاومات الثلاثة السابقة يمكن تحويلها الي ثلاث مقاومات متصلة على شكلY كما بالشكل (b) .
الشكل (a) و الشكل (b) متكافئان كهربيا اذا كانت المقاومة بين أي نقطتين متساوية. و لإيجاد شروط التساوي نعتبر أولا الشكل (a)بين النقطتين2 ,1 يوجد فرعان متصلان على التوازي مقاومة الفرع الأول R12 و مقاومة الفرع الثاني هي R23 , R31 و بذلك تكون المقاومة الكلية بين النقطتين 2 ,1 هي
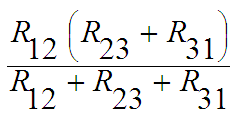
و ألان باعتبار الشكل(b) نجد أن المقاومة بين نفس النقطتين 2 ,1 هي
R1 + R2
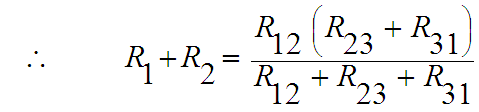(1)
بالنسبة للنقطتين3 ,2 نجد أن
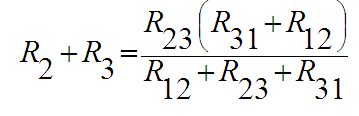(2)
أيضا بالنسبة للنقطتين 3,1 نجد أن
(3)
بطرح (2) من (3) و إضافة الناتج الى (1)
و بطرح (1) من (3) و إضافة الناتج الى (2)
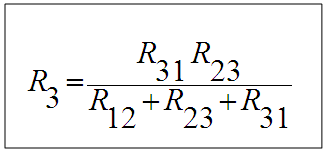
و بالتعويض عن قيمة R3 في (2)
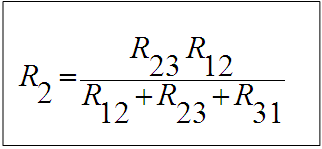
ثانيا: تحويل Δ Y →
و هي حالة عكسية للحالة السابقة. و يمكن الحصول على شروط هذا التحويل بحل المعادلات (3), (2), (1) السابقة آنيا مع بعضها البعض. و بذلك يمكننا الحصول على :
الاكثر قراءة في الكهربائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
الآخبار الصحية
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
