Momentum and Angular Momentum

There is another concept which is very useful in discussing motion, namely momentum. We are all familiar with the qualitative idea of momentum; a body with high momentum, for example a moving car or a bullet in flight, requires a large force to bring it to rest or, to put it another way, the moving body exerts a large force on whatever is stopping it. Momentum is clearly related to the mass of the body, its speed and its direction of motion. Its magnitude is, in fact, simply the product of the mass of a body and its velocity, where by velocity we mean the speed of the body and also its direction of motion. Denoting the magnitude of momentum by p, mass by m and velocity by v we can therefore write

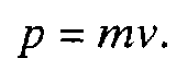
Velocity is another vector quantity since it has magnitude and direction and so, therefore, is momentum a bullet with high momentum has a very different effect when travelling towards you than when travelling away. Momentum is also a quantity which is conserved. This follows from Newton’s laws of motion and, as we delve more deeply into physics, we shall come across many quantities which are conserved-they obey what are known as conservation laws. In the case of momentum, conservation means that, if we have a system of bodies interacting with each other but on which no external force is acting, then the total momentum of the system remains constant. By total momentum is meant the sum of the momenta of the different bodies taking into account their directions of motion. For example, consider a billiard ball with a certain momentum striking another ball at rest in a head on collision. If we neglect the friction between the balls and the surface (i.e. assume no external force) then, after the collision, the sum of their momenta in the direction of the line of impact will be equal to the momentum of the initial ball. Alternatively, consider the firing of a gun. Initially it is at rest and there is zero momentum. After firing it, the forward momentum of the bullet must be compensated for exactly by a backwards momentum of the gun. Hence the recoil of the gun. However, because the gun has a much larger mass than the bullet, a backward momentum equal to that of the bullet is achieved with a much lower speed of recoil than that of the bullet. The same argument applies to the propulsion of a rocket in space the backwards momentum of the ejected burning fuel is compensated for by the forward momentum of the rocket. Similarly conservation of momentum leads to the mishap that may occur when you jump from an unmoored boat onto dry land: the boat moves away from the land as you jump towards it! There is another type of momentum which is extremely important in many aspects of physics, not least the quantum understanding of atoms and nuclei, namely angular momentum. It is a measure of the vigour with which a body rotates. Take the simple example of a heavy weight being rotated by hand in a circle on the end of a piece of string (see figure 1.1(a)). It is common experience that the strength needed to keep the weight rotating increases when a heavier weight is used, the circle is larger or the weight’s speed is faster. The natural propensity is for the weight to shoot off in a staight line and it is the central inward force due to the hand and string known as the centripetal force which holds it in its ‘orbit’. The heavier the weight, the faster it moves or the further it is away from the centre of rotation the greater the force needed and the greater the angular momentum of the weight. In the case of such a rotating weight, the magnitude of its angular momentum is simply defined as the magnitude of its momentum (mv) multiplied by its distance (r) from the centre of rotation, namely mvr. It can be seen that if any of m, v or r are increased, then the angular momentum increases. Angular momentum also applies to spinning bodies such as a top and is simply the sum of the angular momenta of all its component particles about its axis of rotation. To rotate an object, for example a top, requires a twisting force (technically referred to as a torque). Just as a force changes the

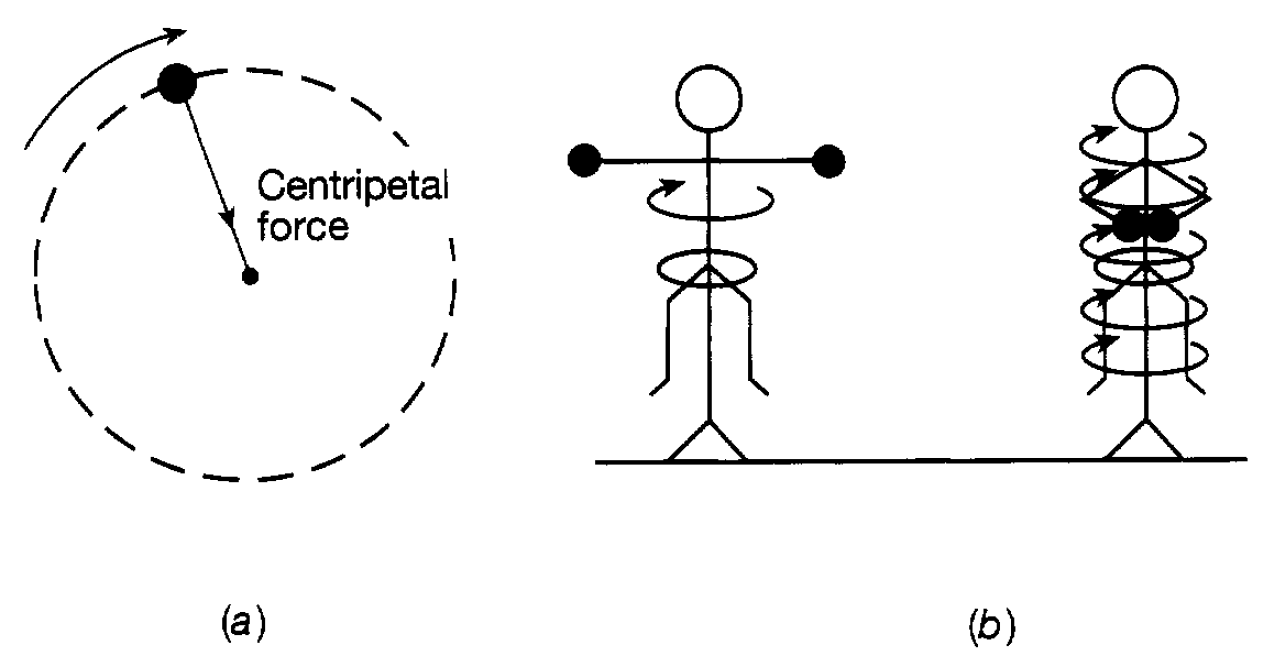
Figure 1.1: (a) A rotating weight. (b) A rotating person.

momentum of an object, a torque changes its angular momentum. Similarly, just as momentum is conserved when no force is acting on a system, so angular momentum is conserved when there is no torque. This is exemplified most dramatically when a person rotates on a stool which can revolve (see figure 1.1(b)). Imagine that the person is set into a spin with arms outstretched and holding a heavy weight in each hand. Now imagine the arms brought into the body. The angular momentum would reduce since the weights are now nearer the axis of rotation. But this cannot happen since there is no torque on the body it is rotating freely and so the only way of conserving the angular momentum of the body is for the speed of rotation to increase. This same phenomenon is seen when ice skaters start a spin with arms outstretched and then bring them into their sides. The examples chosen to illustrate the role of angular momentum have all been simple in the sense that the rotations considered have all been essentially circular the objects considered have rotated at a fixed distance from the axis of rotation. In many situations in nature more complicated rotational motion occurs. For example, the motion of a planet about the sun, which is held in orbit by the gravitational force between them, is elliptical, not circular. Suffice it to say here that, although more complicated in detail, the nature of such motion can again be readily understood in terms of angular momentum and its conservation.