حركة المقذوفات (Projectile Motion)

المقذوفات هي أجسام ترمي في الفضاء إلى الأعلى أو إلى الأسفل ولذلك فإن حركتها هي حركة مركبة تمثل حركة على المحور السيني وأخرى على المحور الصادي وتتصف بالمواصفات التالية:

1- حركة الجسم على المحور السيني تكون بسرعة ثابتة (التسارع = صفراً).

2- حركة الجسم على المحور الصادي تكون مشابهة لحركة السقوط الحر بتسارع ثابت وهو تسارع الجاذبية الأرضية.

3- مقاومة الهواء تعتبر مهملة.

وعلى هذا الاساس فإن الجسم مبدئياً يقذف في الفضاء بمتجه سرعة أولية مقداره v₀ الذي يميل عن الأفق (المحور السيني) بزاوية θ كما في الشكل (1-1).

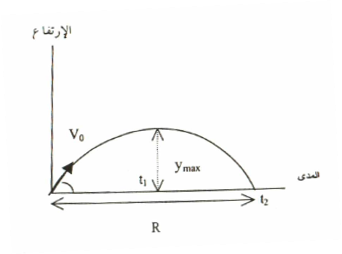
الشكل (1-1)

واستناداً إلى ما ذكر اعلاه يجب ملاحظة الأمور التالية:

t₀ = 0 ، y₀ = 0 ، x₀ = 0 ، a_x = 0 ، a_y = -g

اما بالنسبة لمتجه السرعة الأولية فيمكن تحليله إلى مركبتين إحداهما هي v_x0 = v₀ cosθ (باتجاه المحور السيني)، والثاني هي v_y0 = v_y sinθ (باتجاه المحور الصادي) وحيث أن تسارع الحركتان منتظم ، يمكن تطبيق قوانين الحركة عليهما وبذلك فإن بعض قوانين الحركة على المحور السيني سوف تختصر إلى الشكل التالي:

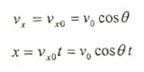
أما فيما يخص الحركة على المحور الصادي فهي تتضمن نفس قوانين السقوط الحر دون تغيير. كذلك يمكن اشتقاق بعض القوانين الخاصة بالمقذوفات حيث أن أقصى ارتفاع تصله المقذوفة يعطى بالمعادلة التالية:

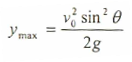
حيث:  sin²θ = sinθ sinθ

كما ان أطول مدى أفقي يمكن أن تصله المقذوفة يعطى بالمعادلة المشتقة التالية:

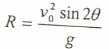
حيث :  sin2θ = 2sinθ cosθ

أن طبيعة الشكل الذي تصنعه المقذوفة في الهواء، يمثل معادلة منحني متناظر (Parabola) ذو صيغة رياضية مماثلة للمعادلة التالية (y = ab – bx²) ولذلك فإن شكل المسار الذي تصنعه المقذوفة يمكن تقسيمه إلى شطرين متناظرين بواسطة مستقيم يمثل الارتفاع الأقصى. وحيث أن شطري مسار المقذوفة متناظران، فإن زمن وصول المقذوفة إلى أقصى ارتفاع (t₁) يساوي زمن وصول المقذوفة من أقصى ارتفاع إلى الأرض وبذلك يمكن القول أن:

t₂ = 2t₁

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل