
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
أنظمة لأكثر من جسيم واحد
المؤلف:
مايكل كوهين
المصدر:
الميكانيكا الكلاسيكية مقدمة أساسية
الجزء والصفحة:
ص 229 – ص 235
2024-10-01
1160
نتجه باهتمامنا الآن إلى الأنظمة المتكونة من أكثر من جسيم (الدليل i يدل على رقم الجسيم). كل جسيم يخضع للمعادلة (4–8)؛ أي إن:
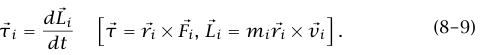
إذا جمعنا معادلات العزم (9–8) لجميع الجسيمات في النظام، فإن العزوم التي تعزى إلى قوى داخلية تلاشى بعضها. وبتعريف كمية التحرك الزاوية الكلية بأنها مجموع كميات التحرك الزاوية للجسيمات المفردة:

افترضنا في اشتقاق المعادلة (11–8) أن  و
و 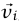 هما موضع وسرعة الجسيم رقم i
هما موضع وسرعة الجسيم رقم i
في إطار قصوري. في الحقيقة، المعادلة (11–8) صحيحة أيضًا إذا استخدمنا محاور غير دوارة (بالنسبة إلى النجوم البعيدة) ونقطة الأصل لها هي مركز كتلة النظام، مثل هذه المحاور لا تكون إطارًا قصوريًّا إذا كان مركز الكتلة متسارعا (متحركًا بعجلة، ولكنها عادة ما تكون أنسب المحاور.
معادلة القوة (20–4) 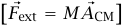 ومعادلة العزم (11–8) تحددان الحركة تمامًا إذا كان النظام جسمًا جاسئًا وهدفنا هنا هو تطوير أساليب لحل المسائل البسيطة، محافظين على أن تكون الرياضيات أبسط ما يمكن؛ لهذا سوف نقصر اهتمامنا أساسًا على الجسم الجاسئ «ذي البُعدين» الذي يتحرك دائما في مستوى الصفحة، ويمكن إهمال سمكه في الاتجاه العمودي على هذه الصفحة. يمكن تطبيق التحليل أيضًا على الأجسام الجاسئة التي لا يمكن إهمال سمكها، بشرط أن تكون جميع حركات الجسم موازيةً لمستوى ثابت، وأن يمتلك الجسم تماثلا كافيًا.
ومعادلة العزم (11–8) تحددان الحركة تمامًا إذا كان النظام جسمًا جاسئًا وهدفنا هنا هو تطوير أساليب لحل المسائل البسيطة، محافظين على أن تكون الرياضيات أبسط ما يمكن؛ لهذا سوف نقصر اهتمامنا أساسًا على الجسم الجاسئ «ذي البُعدين» الذي يتحرك دائما في مستوى الصفحة، ويمكن إهمال سمكه في الاتجاه العمودي على هذه الصفحة. يمكن تطبيق التحليل أيضًا على الأجسام الجاسئة التي لا يمكن إهمال سمكها، بشرط أن تكون جميع حركات الجسم موازيةً لمستوى ثابت، وأن يمتلك الجسم تماثلا كافيًا.
إذا رسمنا خطًا على جسم جاسئ أحادي البعد، فسوف يكون لهذا الخط، عموما، موضع واتجاه مختلفان عند زمن t + Δt مقارنةً بموضعه واتجاهه عند زمن t. في شكل (8–4) يمثل المنحنيان المتصل والمتقطع شكل الجسم عند الزمنين t، وt + Δt على التوالي. لتكن الزاوية بين اتجاهي خطَّي الزمن الابتدائي (الزمن t) والزمن النهائي (الزمن t + Δt) هي Δθ؛ نقيس Δθ بالتقدير الدائري ونسمي Δθ موجبةً إذا كان هناك دوران مع عقارب الساعة يحمل الخط من اتجاهه الابتدائي إلى اتجاهه النهائي، ونسميها سالبة إذا كان الدوران في عكس اتجاه عقارب الساعة.

شكل 8–4: جسم ذو بعدين يُدار بزاوية.
سرعة الجسم الزاوية ω تعرف على الصورة:

قيمة ω الناتجة لا تعتمد على ما هو الخط الذي رسمناه على الجسم؛ لأن كل الخطوط تدور نفس الزاوية نتيجة لحقيقة أن الجسم جاسئ.
افترض نقطة ما O للجسم أُبقي عليها ثابتة (الطريقة الواضحة لعمل ذلك أن تمرر محورًا، عموديًّا على الصفحة خلال الجسم عند O). نختار لمحاورنا إطارًا قصوريًا نقطة الأصل له عند O. ما هي كمية التحرك الزاوية 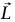 للجسم حول نقطة الأصل O؟ كل نقاط الكتلة تتحرك في دوائر حول O (شكل 8–5)؛ لأن بعدها عن O لا يمكن أن يتغير. وهكذا فإن النقطة الكتلية التي يكون بعدها المتجهي عن O هو
للجسم حول نقطة الأصل O؟ كل نقاط الكتلة تتحرك في دوائر حول O (شكل 8–5)؛ لأن بعدها عن O لا يمكن أن يتغير. وهكذا فإن النقطة الكتلية التي يكون بعدها المتجهي عن O هو  يكون مقدار متجه سرعتها
يكون مقدار متجه سرعتها 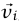 هو |vi = |ωri واتجاهه عموديا على
هو |vi = |ωri واتجاهه عموديا على  . شكل 8–5 يوضح حالة ω موجبة (دوران في اتجاه عقارب الساعة)، إذا كانت O سالبة، فإن
. شكل 8–5 يوضح حالة ω موجبة (دوران في اتجاه عقارب الساعة)، إذا كانت O سالبة، فإن 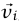 تكون في الاتجاه المعاكس. وفي كلتا الحالتين:
تكون في الاتجاه المعاكس. وفي كلتا الحالتين:


شكل 8–5: سرعة النقطة الكتلية في جسم جاسئ دوار.

وبالنسبة للأجسام ذات الثلاثة أبعاد (تشمل كرة مركزها O) ولها تماثل كافٍ حول O، فإن المعادلتين (14–8) و(15–8) لا تزالان ساريتين بشرط أن يكون 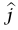 هو محور الدوران (وفي المعادلة (15–8)) ri يحل محلها
هو محور الدوران (وفي المعادلة (15–8)) ri يحل محلها  ، المسافة العمودية من محور الدوران حتى mi.
، المسافة العمودية من محور الدوران حتى mi.
عادة ما يسمى I عزم القصور الذاتي للجسم حول المحور 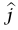 خلال نقطة الأصل O. يسمى I أحيانًا «القصور الدوراني» للجسم. وهذا مصطلح ممتاز؛ لأن I في الحقيقة هي مقياس لمدى صعوبة تغير السرعة الزاوية لجسم ما مثلما أن M مقياس لمدى صعوبة تغير السرعة الخطية.
خلال نقطة الأصل O. يسمى I أحيانًا «القصور الدوراني» للجسم. وهذا مصطلح ممتاز؛ لأن I في الحقيقة هي مقياس لمدى صعوبة تغير السرعة الزاوية لجسم ما مثلما أن M مقياس لمدى صعوبة تغير السرعة الخطية.
في مسألة ذات بعدين يكون العزم عموديًا على الصفحة 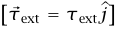 وبهذا تصبح المعادلة τext = Idω/dt. بتعريف العجلة الزاوية α = dω/dt نحصل على:
وبهذا تصبح المعادلة τext = Idω/dt. بتعريف العجلة الزاوية α = dω/dt نحصل على:

المعادلة (16–8) هي «الوصفة العلاجية» التي كنا ننشدها؛ فهي تربط العجلة الزاوية لجسم جاسئ بالعزم المؤثر على الجسم، وهي تناظر بوضوح قانون نيوتن الثاني (بإحلال العزم محل القوة، والعجلة الزاوية محل العجلة الخطية، والقصور الدوراني محل الكتلة).
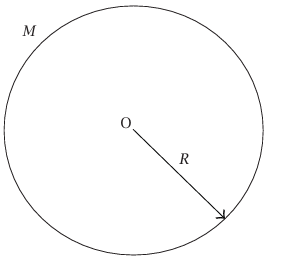
شكل 8–6: طوق كتلته M ونصف قطره R.
نحتاج لاستخدام المعادلة (16–8) أن نعرف عزوم القصور الذاتي لبعض الأجسام الجاسئة البسيطة:
(أ) عزم قصور لطوق (كتلته m ونصف قطره R) حول مركزه (شكل 8–6). الكتلة كلها في هذه الحالة على نفس المسافة من نقطة الأصل O وبهذا يكون:

(ب) عزم قصور قرص منتظم (كتلته M ونصف قطره R) حول مركزه. في هذه الحالة تكون عناصر كتلية مختلفة على أبعاد مختلفة من نقطة الأصل. إذا قسمنا الجسم إلى حلقات عديدة (شكل 8–7)، فإن مساحة الحلقة المحدودة بدائرتين نصفا قطريهما r وr + dr هي 2πrdr، وكتلة هذه الحلقة هي 2πrdr)σ)؛ حيث σ هي كتلة وحدة المساحات. عزم القصور هو:
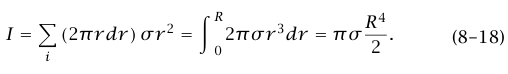
كتلة القرص هي M = πR2σ، وبهذا يكون I = (1/2)MR2. المعادلة (18–8) يكون لها معنى عند مقارنتها بالمعادلة (17–8)؛ لأنه في حالة القرص المنتظم يكون البعد «المتوسط» لعناصر الكتلة عن المركز أقل من R.
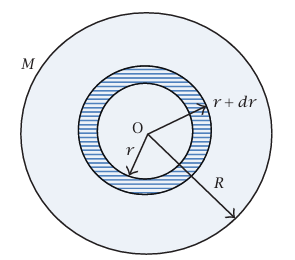
شكل 8–7: قرص مسطح نصف قطره R وكتلته M.
(جـ) عزم قصور قضيب منتظم (كتلته M وطوله L) حول أحد طرفيه. اعتبر جزءًا صغيرًا من القضيب طوله dx وكتلته M/L)dx) (انظر شكل 8–8). إذا قيس البعد x عن طرف القضيب، نجد أن:

(د) عزم قصور طوق أو قرص منتظم حول نقطة على حافة (نحتاج إلى هذا إذا رغبنا في تطبيق المعادلة (16–8) على جسم يتدحرج بدون انزلاق على منحدر باستخدام نقطة التماس كنقطة أصل). في هذه الحالات يصعب إجراء التكامل. ومع ذلك، فإن نظرية بسيطة تمكننا من كتابة الإجابة فورًا بدلالة نتيجتي (أ) و(ب).

شكل 8–8: قضيب طوله L وكتلته M.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















