
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
الاحتكاك
المؤلف:
مايكل كوهين
المصدر:
الميكانيكا الكلاسيكية مقدمة أساسية
الجزء والصفحة:
ص 68 – ص 73
2024-09-12
1531
عندما يكون سطحا جسيمين متماسين؛ فانه كثيرا ما تكون هذه هي الحالة التي لا يكون فيها للقوة التي لا يؤثر بها احد الجسمين على الاخر مركبة عمودية على السطح فقط، ولكن لها مركبة موازية للسطح. هذه الاخيرة تسمى قوة الاحتكاك، وهي تلعب دورا رئيسيا في العديد من الظواهر المألوفة. فمثلا، لا يمكن قيادة سيارة اعلى تل، او حتى ايقافها على تل، اذا لم يكن الاحتكاك موجودا. لا يمكن للسيارة كذلك أن تجتاز ملفا ما. في غياب الاحتكاك، سينزلق راكب ما يقف في عربة سكة حديد نحو الجزء الخلفي من العربة عندما يتسارع القطار. لقد اعتدنا اعتقاد أن الاحتكاك هو شيء غير مرغوب (ونقوم بانفاق قدر كبير من المال على عمليات التشحيم لتقليل قوة الاحتكاك التي تكون موجودة عندما ينزلق سطح ما على آخر)، لكن الأمثلة السابقة توضح أن الاحتكاك كثيرًا ما يكون أمرًا مرغوباً وأساسيًّا.
ما من داع للتشديد على أن صحة قوانين نيوتن لا تتطلب الافتراض غير الواقعي المتمثل في وجود عالم خالٍ من الاحتكاك. تَصِفُ قوانين نيوتن العالم الواقعي بقواه الواقعية. صحيح أننا نفترض في بعض المسائل عدم وجود احتكاك، لكن هذا ليس ضروريًا من الناحية المفاهيمية. لم يُدرك معظم أسلاف نيوتن أن الحفاظ على جسم ما متحركا بسرعة ثابتة لا يتطلب أي قوة؛ فقد لاحظوا أنه لجعل جسم ما يستمر في الحركة على منضدة أفقية، يجب عليهم دفعه. لا يعني هذا ضمنًا أن قانون نيوتن الأول خاطئ؛ فالدفع الضروري يكون ببساطة مساويًا ومضادا لقوة الاحتكاك المؤثرة بواسطة المنضدة. واليوم، مع المسارات الهوائية والمناضد الهوائية التي تجعل بالفعل قرصا أو ناقلة معلقة فوق سطح ما بواسطة وسادة رفيعة من الهواء، يمكننا الاقتراب جدًّا من تحقيق حالة سطح بدون احتكاك تجريبيا. لا يعتقد أي شخص قام بتجربة المسار الهوائي أو المنضدة الهوائية أن من الضروري وجود قوة للإبقاء على جسم ما متحرگا.
إن الأصل الميكروسكوبي لقوى الاحتكاك لم يُفهم بعد على نحو كامل، كما أن هذا الفهم ليس ضروريًا لأغراضنا. في بعض الحالات يمكن حساب مقدار قوى الاحتكاك بدون حتى معرفة أي شيء عن طبيعة الأسطح. في حالات أخرى يكون من الضروري معرفة المزيد عن الأسطح (أي تركيبها ودرجة ملاستها). إن اعتبار بضعة أمثلة بسيطة ربما يكون أكثر تنويرًا من المناقشة النظرية المجردة لهذا الموضوع.
مثال 2–9 (كتلة على منضدة مع احتكاك) اعتبر كتلة ساكنة على منضدة أفقية (شكل 2–14). القوتان الوحيدتان اللتان تؤثران على الكتلة هما قوة الجاذبية 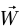 (متجهة إلى أسفل) والقوة العمودية
(متجهة إلى أسفل) والقوة العمودية 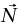 (متجهة إلى أعلى) المؤثرة بواسطة المنضدة. يتطلب قانون نيوتن الأول أن يكون
(متجهة إلى أعلى) المؤثرة بواسطة المنضدة. يتطلب قانون نيوتن الأول أن يكون 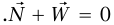 والآن افترض أن قوةً ما أفقية أثرت على الكتلة. نعلم من خبرتنا أن الكتلة ستظل ساكنة على منضدة واقعية (أي منضدة ليست ملساء تمامًا) إذا كان مقدار
والآن افترض أن قوةً ما أفقية أثرت على الكتلة. نعلم من خبرتنا أن الكتلة ستظل ساكنة على منضدة واقعية (أي منضدة ليست ملساء تمامًا) إذا كان مقدار 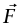 ليس كبيرًا جدًّا.
ليس كبيرًا جدًّا.
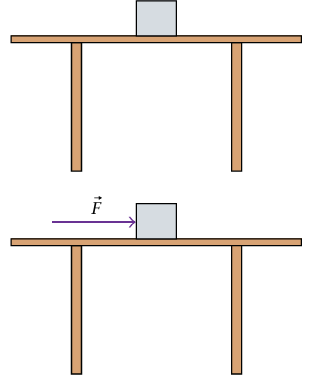
قانون نيوتن الأول يتطلب حتمية وجود قوة أفقية أخرى، مساوية في المقدار ومضادة في الاتجاه لـ 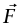 تؤثر على الكتلة. هذه القوة، التي تؤثر بواسطة سطح المنضدة على السطح السفلي للكتلة، تسمى قوة الاحتكاك ويرمز لها بالرمز
تؤثر على الكتلة. هذه القوة، التي تؤثر بواسطة سطح المنضدة على السطح السفلي للكتلة، تسمى قوة الاحتكاك ويرمز لها بالرمز 
شكل 2–14: توضيح لمثال 2–9.
ينص قانون نيوتن الأول على أن 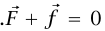 (النص الكامل للقانون الأول في هذه الحالة هو
(النص الكامل للقانون الأول في هذه الحالة هو 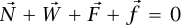 لكن بما أن
لكن بما أن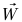 و
و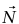 قوتان رأسيتان و
قوتان رأسيتان و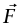 و
و أفقيتان، فينتج من ذلك أن
أفقيتان، فينتج من ذلك أن  ) ولتبسيط التصور، يمكن للمرء أن يتخيَّل أن سطحي كلٌّ من المنضدة والكتلة بهما خشونة صغيرة (قمم ومنخفضات)، بحيث يتشابك السطحان إلى حَدٍّ ما، مثل مجموعة من أسنان التروس (شكل 2–15). إن قوة الاحتكاك هي ببساطة القوة الأفقية التي تؤثر بواسطة خشونة المنضدة على خشونة الكتلة.
) ولتبسيط التصور، يمكن للمرء أن يتخيَّل أن سطحي كلٌّ من المنضدة والكتلة بهما خشونة صغيرة (قمم ومنخفضات)، بحيث يتشابك السطحان إلى حَدٍّ ما، مثل مجموعة من أسنان التروس (شكل 2–15). إن قوة الاحتكاك هي ببساطة القوة الأفقية التي تؤثر بواسطة خشونة المنضدة على خشونة الكتلة.
طالما أن الكتلة في مثال 2–9 ساكنة ؛ فإن المقدار f لقوة الاحتكاك يساوي ببساطة المقدار F للقوة المؤثّرة. لقد حسبنا f في هذه الحالة دون معرفة أي شيء عن طبيعة السطحين.
السؤال البديهي هو: ما القدر الذي ينبغي أن تؤثر به قوة F لجعل الكتلة تنزلق؟ بالطبع تعتمد الإجابة على المواد المصنوعة منها الكتلة والمنضدة، وأيضًا على درجة نعومة السطحين. وحتى إذا كُنَّا نعلم تركيب ودرجة نعومة كلٌّ من السطحين، فإنه من المستحيل عمليا الإجابة على هذا السؤال من المبادئ الأولى؛ لأنه يتطلب فهما تفصيليا للتآثرات المختلفة على المقياس الميكروسكوبي (الجزيئي). لحسن الحظ، يمكن الإجابة على السؤال تجريبيا ويمكن تلخيص كَمِّيَّة هائلة من البيانات بواسطة «قانون» بسيط جدًّا. نؤكد على أن هذا القانون ليس جوهريا (على عكس قوانين نيوتن)، لكنه يوفر ملخصا مفيدًا للبيانات التجريبية.
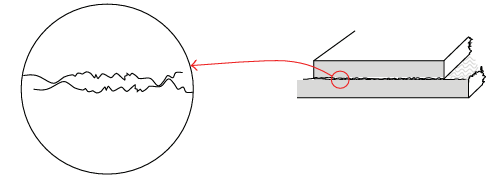
شكل 2–15: تمثيل تخطيطي لمنشأ الاحتكاك الاستاتيكي. في الواقع، خشونة السطحين أصغر بكثير مما هو مبين هنا، لكنها موجودة حتى للأسطح ناعمة الملمس.
على وجه العموم، عندما يكون سطحًا جسمين متماسين؛ فإن الجسم A يؤثر بقوة عمودية  (متعامدة مع السطح) وقوة احتكاك
(متعامدة مع السطح) وقوة احتكاك  (موازية للسطح) على الجسم B، ويتطلب قانون نيوتن الثالث أن يؤثر B بقوتين
(موازية للسطح) على الجسم B، ويتطلب قانون نيوتن الثالث أن يؤثر B بقوتين  – و
– و – على A. نرمز لمقدار
– على A. نرمز لمقدار  (و
(و –) بالرمز N ومقدار
–) بالرمز N ومقدار  ( و
( و –) بالرمز f. في مثال 2–9، N تساوي وزن الكتلة W و f تساوي المقدار F للقوة المؤثرة. يمكن تغيير N عن طريق وضع أوزان إضافية فوق الكتلة. يمكننا قياس Fmax لكلٌّ من قيم N، وهي أكبر قيمة لـ F يمكن تطبيقها دون أن تتسبب في انزلاق الكتلة. وجد أن النسبة Fmax/N تظل ثابتة مع تغير N. تسمى هذه النسبة معامل الاحتكاك الاستاتيكي بين السطحين ويرمز لها بالرمز sμ.
–) بالرمز f. في مثال 2–9، N تساوي وزن الكتلة W و f تساوي المقدار F للقوة المؤثرة. يمكن تغيير N عن طريق وضع أوزان إضافية فوق الكتلة. يمكننا قياس Fmax لكلٌّ من قيم N، وهي أكبر قيمة لـ F يمكن تطبيقها دون أن تتسبب في انزلاق الكتلة. وجد أن النسبة Fmax/N تظل ثابتة مع تغير N. تسمى هذه النسبة معامل الاحتكاك الاستاتيكي بين السطحين ويرمز لها بالرمز sμ.
يعتمد معامل الاحتكاك الاستاتيكي على تركيب ونعومة السطحين، لكنه لا يعتمد على مساحة التماس؛ ولذلك ، إذا استبدل بالكتلة أخرى من المادة نفسها وبدرجة النعومة نفسها لكن لها ضعف مساحة السطح السفلي، فإننا سنجد أن النسبة N/Fmax كما هي، مثل الكتلة الأصلية. (يمكن استنتاج حقيقة أن N/Fmax لا تتغير مع تغير مساحة التماس A من حقيقة أن N/Fmax لا تعتمد على N عند ثبوت A. تُرك البرهان كتحدٍّ للقارئ المهتم.) وبما أن F = f طالما أن الكتلة لا تنزلق، فينتج من ذلك أن Fmax = fmax؛ حيث fmax هي أعلى قيمة لقوة الاحتكاك التي يمكن لسطح ما أن يؤثر بها على الاخر (بالنسبة لقسمة معينة من القوة العادية).
وبهذا نصل الى «القانون» التجريبي للاحتكاك الاستاتيكي: عندما يوجد سطحان متماسان دون ان يتحرك احدهما على الاخر (أي دون انزلاق)، فإن القيمة العظمى لقوة الاحتكاك التي يمكن ان يؤثر بها احد السطحين على الاخر تتناسب طرديا مع القوة العمودية، ويعتمد مقدار التناسب sμ فقط على تركيب ونعومة السطحين؛ أي:

نؤكد على أن المعادلة (1–2) «متباينة رياضياتية». يتحقق التساوي فقط عندما يوشك الانزلاق على الحدوث. يقع الكثير من الطلبة في عادة استبدال μs N بـ f تلقائيا مما يؤدي إلى نتائج كارثية. فمثلا إذا لم يكن هناك قوة أفقية F مؤثرة على الكتلة في مثال 2–9، فلن يكون هناك قوة احتكاك وستكون النسبة N/f صفرًا حتى لو لم يكن sμ صفرًا.
مثال 2–10 (كتلة على منحدر مع احتكاك). كتلة وزنها 100 نيوتن (N) مستقرة في حالة اتزان على مستوى مائل بزاوية 30o. ومعامل الاحتكاك الاستاتيكي بين المستوى والكتلة هو = 0.6sμ نرغب في حساب قوة الاحتكاك والقوة العمودية المؤثرة على الكتلة بواسطة المستوى.
مخطط الجسم الحر للكتلة مبين في شكل 2–16. وبأخذ مركبتين لمعادلة القوة على طول المحورين الموازي والعمودي على المستوى، نحصل على
0 = °30 f – (100n) sin و0 = °30 cos (n100) – N. وبهذا يكون n50f = وN = 86.6n.
لاحظ أننا لم نستخدم قيمة μs المعطاة. تدخل قيمة μs في المناقشة فقط إذا سألنا: «هل يمكن فعلًا للكتلة أن تكون في حالة اتزان على المستوى؟» باختبار النسبة f/N، نجد أن 0.577 = °30 f/N = tan؛ ولذلك نجد من المعادلة (12–2) أن الاتزان ممكن؛ لأن 0.6 > 0.577 بشكل أعم، إذا كانت كتلة ما وزنها W في حالة اتزان على مستوى مائل يصنع زاوية θ مع الأفقي، فإن قوة الاحتكاك هي θ f = W sin والقوة العمودية هي θ W cos = N. وهكذا نجد أن f/n = tan θ وبذلك يكون الاتزان الاستاتيكي ممكنا فقط إذا كان tan θ ≤ μs s
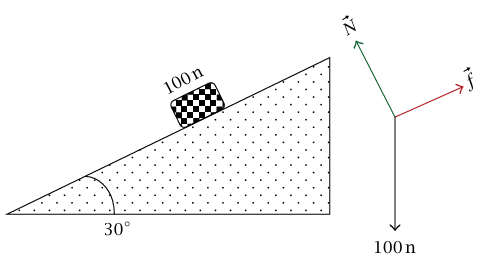
شكل 2–16: الرسم التوضيحي ومخطط الجسم الحر لمثال 2–10.
في المثال السابق، أقصى زاوية يكون عندها الاتزان الاستاتيكي ممكنا هي °31= (0.6) 1–θmax = tan. لقد افترضنا ضمنًا أنه بزيادة θ نصل إلى أن الكتلة تبدأ في الانزلاق لأسفل المستوى من المحتمل أيضًا أن تنقلب الكتلة قبل أن تبدأ في الانزلاق.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















