المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
الفيزياء الكلاسيكية
الكهربائية والمغناطيسية
علم البصريات
الفيزياء الحديثة
النظرية النسبية
الفيزياء النووية
فيزياء الحالة الصلبة
الليزر
علم الفلك
المجموعة الشمسية
الطاقة البديلة
الفيزياء والعلوم الأخرى
مواضيع عامة في الفيزياء| الحركة الدائرية: الطريقة التحليلية |
 310
 01:21 صباحاً
التاريخ: 2024-09-05 |
المؤلف : مايكل كوهين 
الكتاب أو المصدر : الميكانيكا الكلاسيكية مقدمة أساسية 
الجزء والصفحة : ص 30 – ص 32|
أقرأ أيضاً
التاريخ: 31-8-2017
5071
التاريخ: 2024-01-31
842
التاريخ: 2024-02-13
707
التاريخ: 9-2-2016
2317
|
إذا أدخلنا متجهي الوحدة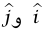 
شكل (1–13) تكون الصورة المتجهية من مركز الدائرة حتى الموضع اللحظي للجسيم هي 
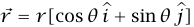، حيث r وθ هما الإحداثيان القطبيان المعتادان. إذا كان الجسيم يتحرك في دائرة بمقدار سرعة ثابت يكون 0 = dr/dt وdθ/dt = constant (ثابت). إذن:
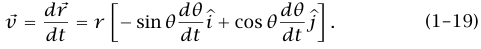
لقد استخدمنا قاعدة السلسلة [d/dθ (cos θ)][dθ/dt] = (θ d/dt(cos وهكذا. لاحظ أن معادلات التفاضل القياسية تتطلب أن تكون θ مُعَبَّرًا عنها بالتقدير الدائري. ينبغي أيضًا أن يكون واضحًا أن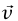 
متجه مماسي للدائرة. لاحظ أن 
وبهذا يكون:
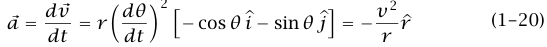
وهو مثل ما تم استنتاجه أعلاه بالطريقة الهندسية.
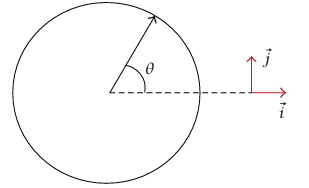
الشكل 1-13: انشاء هندسي لعجلة حركة دائرية ذات مقدار سرعة ثابتة
|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|
