We have now effect which occurs in air as a consequence of the irregular positions of the atoms. When we were discussing the index of refraction, we saw that an incoming beam of light will make the atoms radiate again. The electric field of the incoming beam drives the electrons up and down, and they radiate because of their acceleration. This scattered radiation combines to give a beam in the same direction as the incoming beam, but of somewhat different phase, and this is the origin of the index of refraction.
But what can we say about the amount of re-radiated light in some other direction? Ordinarily, if the atoms are very beautifully located in a nice pattern, it is easy to show that we get nothing in other directions, because we are adding a lot of vectors with their phases always changing, and the result comes to zero. But if the objects are randomly located, then the total intensity in any direction is the sum of the intensities that are scattered by each atom, as we have just discussed. Furthermore, the atoms in a gas are in actual motion, so that although the relative phase of two atoms is a definite amount now, later the phase would be quite different, and therefore each cosine term will average out. Therefore, to find out how much light is scattered in a given direction by a gas, we merely study the effects of one atom and multiply the intensity it radiates by the number of atoms.
Earlier, we remarked that the phenomenon of scattering of light of this nature is the origin of the blue of the sky. The sunlight goes through the air, and when we look to one side of the sun—say at 90∘ to the beam—we see blue light; what we now have to calculate is how much light we see and why it is blue.
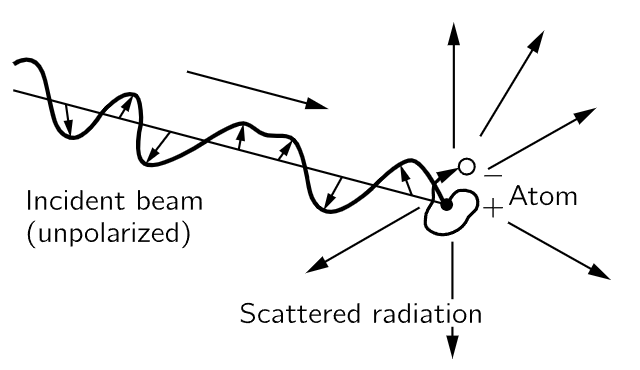
Fig. 32–2. A beam of radiation falls on an atom and causes the charges (electrons) in the atom to move. The moving electrons in turn radiate in various directions.
If the incident beam has the electric field 1 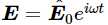 at the point where the atom is located, we know that an electron in the atom will vibrate up and down in response to this E (Fig. 32–2). From Eq. (23.8), the response will be
at the point where the atom is located, we know that an electron in the atom will vibrate up and down in response to this E (Fig. 32–2). From Eq. (23.8), the response will be
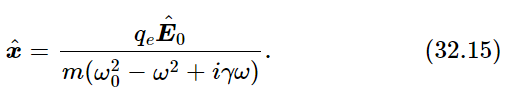
We could include the damping and the possibility that the atom acts like several oscillators of different frequency and sum over the various frequencies, but for simplicity let us just take one oscillator and neglect the damping. Then the response to the external electric field, which we have already used in the calculation of the index of refraction, is simply

We could now easily calculate the intensity of light that is emitted in various directions, using formula (32.2) and the acceleration corresponding to the above 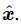
Rather than do this, however, we shall simply calculate the total amount of light scattered in all directions, just to save time. The total amount of light energy per second, scattered in all directions by the single atom, is of course given by Eq. (32.6). So, putting together the various pieces and regrouping them, we get
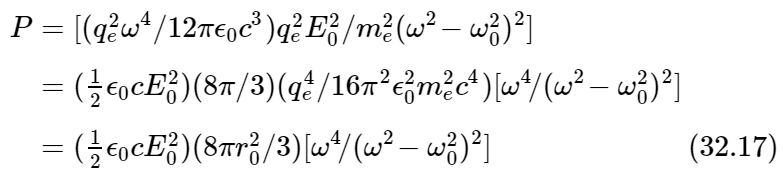
for the total scattered power, radiated in all directions.
We have written the result in the above form because it is then easy to remember: First, the total energy that is scattered is proportional to the square of the incident field. What does that mean? Obviously, the square of the incident field is proportional to the energy which is coming in per second. In fact, the energy incident per square meter per second is ϵ0c times the average ⟨E2⟩ of the square of the electric field, and if E0 is the maximum value of E, then ⟨E2⟩=1/2 E20. In other words, the total energy scattered is proportional to the energy per square meter that comes in; the brighter the sunlight that is shining in the sky, the brighter the sky is going to look.
Next, what fraction of the incoming light is scattered? Let us imagine a “target” with a certain area, let us say σ, in the beam (not a real, material target, because this would diffract light, and so on; we mean an imaginary area drawn in space). The total amount of energy that would pass through this surface σ in a given circumstance is proportional both to the incoming intensity and to σ, and the total power would be
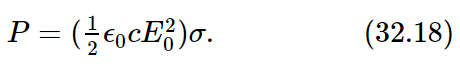
Now we invent an idea: we say that the atom scatters a total amount of intensity which is the amount which would fall on a certain geometrical area, and we give the answer by giving that area. That answer, then, is independent of the incident intensity; it gives the ratio of the energy scattered to the energy incident per square meter. In other words, the ratio
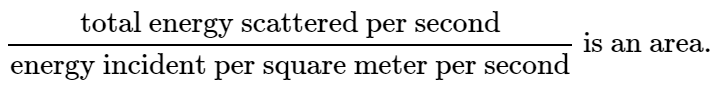
The significance of this area is that, if all the energy that impinged on that area were to be spewed in all directions, then that is the amount of energy that would be scattered by the atom.
This area is called a cross section for scattering; the idea of cross section is used constantly, whenever some phenomenon occurs in proportion to the intensity of a beam. In such cases one always describes the amount of the phenomenon by saying what the effective area would have to be to pick up that much of the beam. It does not mean in any way that this oscillator actually has such an area. If there were nothing present but a free electron shaking up and down there would be no area directly associated with it, physically. It is merely a way of expressing the answer to a certain kind of problem; it tells us what area the incident beam would have to hit in order to account for that much energy coming off. Thus, for our case,
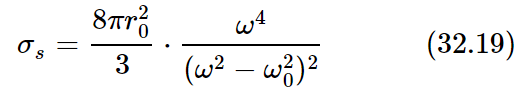
(the subscript s is for “scattering”).
Let us look at some examples. First, if we go to a very low natural frequency ω0, or to completely unbound electrons, for which ω0=0, then the frequency ω cancels out and the cross section is a constant. This low-frequency limit, or the free electron cross section, is known as the Thomson scattering cross section. It is an area whose dimensions are approximately 10−15 meter, more or less, on a side, i.e., 10−30 square meter, which is rather small!
On the other hand, if we take the case of light in the air, we remember that for air the natural frequencies of the oscillators are higher than the frequency of the light that we use. This means that, to a first approximation, we can disregard ω2 in the denominator, and we find that the scattering is proportional to the fourth power of the frequency. That is to say, light which is of higher frequency by, say, a factor of two, is sixteen times more intensely scattered, which is a quite sizable difference. This means that blue light, which has about twice the frequency of the reddish end of the spectrum, is scattered to a far greater extent than red light. Thus, when we look at the sky it looks that glorious blue that we see all the time!
There are several points to be made about the above results. One interesting question is, why do we ever see the clouds? Where do the clouds come from? Everybody knows it is the condensation of water vapor. But, of course, the water vapor is already in the atmosphere before it condenses, so why don’t we see it then? After it condenses it is perfectly obvious. It wasn’t there, now it is there. So the mystery of where the clouds come from is not really such a childish mystery as “Where does the water come from, Daddy?,” but has to be explained.
We have just explained that every atom scatters light, and of course the water vapor will scatter light, too. The mystery is why, when the water is condensed into clouds, does it scatter such a tremendously greater amount of light?
Consider what would happen if, instead of a single atom, we had an agglomerate of atoms, say two, very close together compared with the wavelength of the light. Remember, atoms are only an angstrom or so across, while the wavelength of light is some 5000 angstroms, so when they form a clump, a few atoms together, they can be very close together compared with the wavelength of light. Then when the electric field acts, both of the atoms will move together. The electric field that is scattered will then be the sum of the two electric fields in phase, i.e., double the amplitude that there was with a single atom, and the energy which is scattered is therefore four times what it is with a single atom, not twice! So lumps of atoms radiate or scatter more energy than they do as single atoms. Our argument that the phases are independent is based on the assumption that there is a real and large difference in phase between any two atoms, which is true only if they are several wavelengths apart and randomly spaced, or moving. But if they are right next to each other, they necessarily scatter in phase, and they have a coherent interference which produces an increase in the scattering.
If we have N atoms in a lump, which is a tiny droplet of water, then each one will be driven by the electric field in about the same way as before (the effect of one atom on the other is not important; it is just to get the idea anyway) and the amplitude of scattering from each one is the same, so the total field which is scattered is N-fold increased. The intensity of the light which is scattered is then the square, or N2-fold, increased. We would have expected, if the atoms were spread out in space, only N times as much as 1, whereas we get N2 times as much as 1! That is to say, the scattering of water in lumps of N molecules each is N times more intense than the scattering of the single atoms. So as the water agglomerates the scattering increases. Does it increase ad infinitum? No! When does this analysis begin to fail? How many atoms can we put together before we cannot drive this argument any further? Answer: If the water drop gets so big that from one end to the other is a wavelength or so, then the atoms are no longer all in phase because they are too far apart. So, as we keep increasing the size of the droplets we get more and more scattering, until such a time that a drop gets about the size of a wavelength, and then the scattering does not increase anywhere nearly as rapidly as the drop gets bigger. Furthermore, the blue disappears, because for long wavelengths the drops can be bigger, before this limit is reached, than they can be for short wavelengths. Although the short waves scatter more per atom than the long waves, there is a bigger enhancement for the red end of the spectrum than for the blue end when all the drops are bigger than the wavelength, so the color is shifted from the blue toward the red.
Now we can make an experiment that demonstrates this. We can make particles that are very small at first, and then gradually grow in size. We use a solution of sodium thiosulfate (hypo) with sulfuric acid, which precipitates very fine grains of sulfur. As the sulfur precipitates, the grains first start very small, and the scattering is a little bluish. As it precipitates more it gets more intense, and then it will get whitish as the particles get bigger. In addition, the light which goes straight through will have the blue taken out. That is why the sunset is red, of course, because the light that comes through a lot of air, to the eye has had a lot of blue light scattered out, so it is yellow-red.
Finally, there is one other important feature, on polarization, but it is so interesting that we point it out now. This is that the electric field of the scattered light tends to vibrate in a particular direction. The electric field in the incoming light is oscillating in some way, and the driven oscillator goes in this same direction, and if we are situated about at right angles to the beam, we will see polarized light, that is to say, light in which the electric field is going only one way. In general, the atoms can vibrate in any direction at right angles to the beam, but if they are driven directly toward or away from us, we do not see it. So, if the incoming light has an electric field which changes and oscillates in any direction, which we call unpolarized light, then the light which is coming out at 90∘ to the beam vibrates in only one direction! (See Fig. 32–3.)
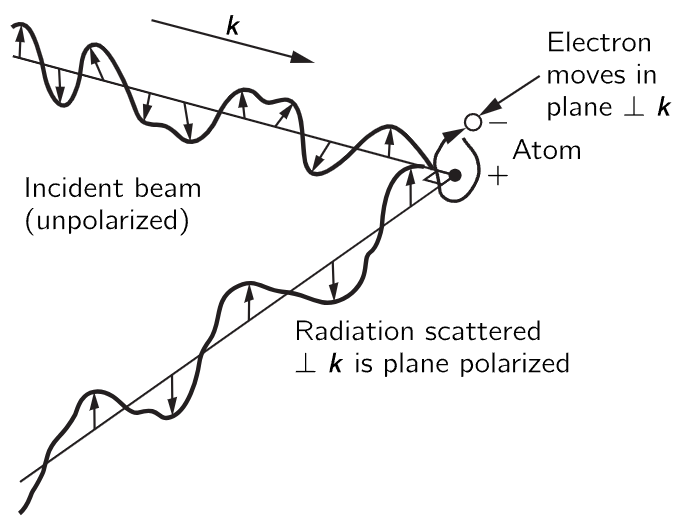
Fig. 32–3. Illustration of the origin of the polarization of radiation scattered at right angles to the incident beam.
There is a substance called polaroid which has the property that when light goes through it, only the piece of the electric field which is along one particular axis can get through. We can use this to test for polarization, and indeed we find the light scattered by the hypo solution to be strongly polarized.
_______________________________________________
Margin
1- When a caret appears on a vector it signifies that the components of the vector are complex: 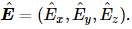
 الاكثر قراءة في الضوء
الاكثر قراءة في الضوء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


