انكسار الضوء خلال المنشور الثلاثي
المؤلف:
محمد جواد جادر النعيمي
المصدر:
الضوء الهندسي
الجزء والصفحة:
21-7-2016
35284
انكسار الضوء خلال المنشور الثلاثي
المنشور الثلاثي هو جزء من وسط شفاف متجانس محدود بسطحين غير متوازيين. فإذا فرضنا أن ABC يمثل المقطع الأساسي لمنشور ثلاثي من الزجاج زاوية رأسه A و أن شعاعا ضوئيا DE يسقط على الوجه AC فانه ينكسر داخل المنشور مقتربا من العمود ( في الاتجاه EF) ثم يخرج من الوجه AB في الاتجاه FG كما بالشكل.
من هذا الشكل يتضح أن الشعاع DE يعانى انحراف كل من النقطتين E و F و أن الانحراف الكلي في اتجاه DE يقدر بقيمة الزاوية بين امتداد الشعاعين DE و GF.
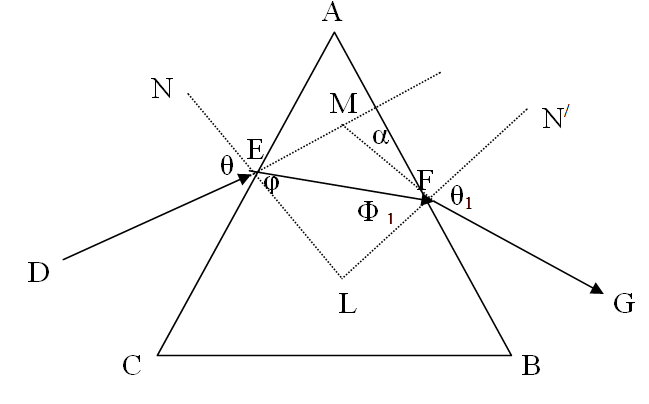
فإذا كانت الزوايا θ و φ و φ1 وθ1 تمثل زوايا السقوط و الانكسار عند النقطتين E و F فان:
(1)
(2)
و زاوية الانحراف α تعطى من
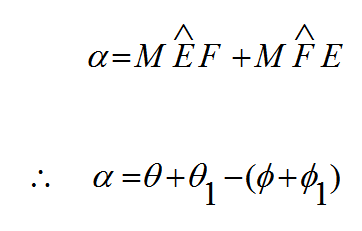(3)
في الشكل الرباعي AELF نجد أن
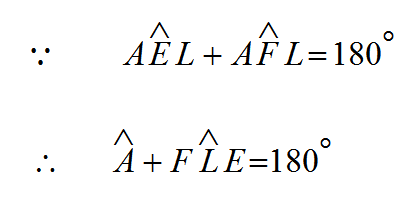(4)
من المثلث FEL نجد أن
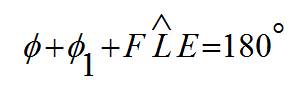
بالتعويض من المعادلة (4) في المعادلة السابقة نحصل على:
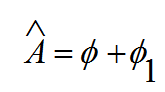(5)
من المعادلتين (3) و (5) نجد أن:
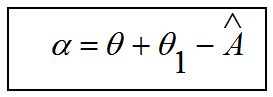(6)
و حيث أن A زاوية رأس المنشور تكون ثابتة لا تتغير إلا بتغير المنشور، فان زاوية الانحراف α تتوقف على زاويتي السقوط و الخروج..
النهاية الصغرى لزاوية الانحراف:-
ذكرنا في المعادلة السابقة أن زاوية الانحراف تتغير تبعا لتغير زاويتي السقوط و الخروج، فإذا رسمت العلاقة بين زاوية الانحراف وزاوية السقوط فسوف يكون لها سلوك كالمماثل بالشكل
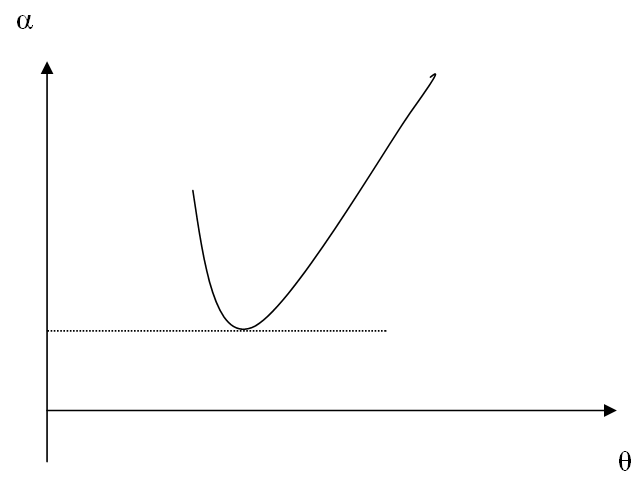
و نلاحظ أنه كلما ذادت زاوية السقوط قلت زاوية الانحراف حتى تصل إلى أقل قيمة لها ثم تأخذ بعدها في الزيادة مرة أخرى، و معنى هذا أن هناك قيمة لزاوية السقوط تكون عندها زاوية الانحراف اقل ما يمكن و تسمى النهاية الصغرى لزاوية الانحراف ورياضيا يعنى هذا أن:
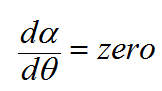
بتفاضل المعادلة (6) بالنسبة ل θ
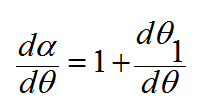(7)
و عند وضع النهاية الصغرى للانحراف يكون
(8)
و بتفاضل المعادلة (5) نحصل على
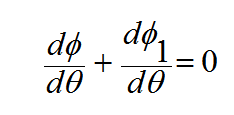(9)
فإذا كان μ معامل انكسار مادة المنشور فان
(*)
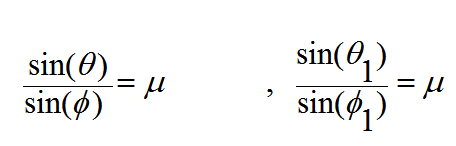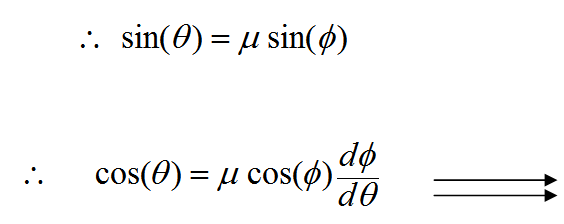
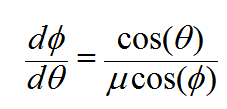(10)
بالمثل يمكننا الحصول على
(11)
بالتعويض من (10) في (9)
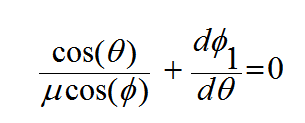(12)
و حيث أن
(13)
بالتعويض من (11) و (12) في (13) نحصل على
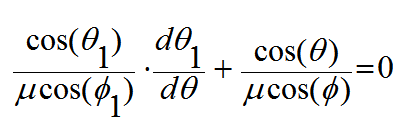(14)
بالتعويض من (8) في (14)
(15)
و من قوانين حساب المثلثات يمكننا كتابة هذه المعادلة على الصورة الآتية
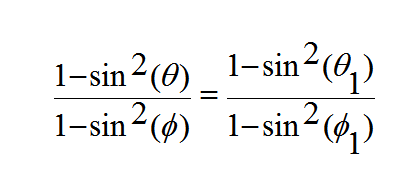(16)
و بالتعويض من المعادلة (*) في المعادلة السابقة نحصل على
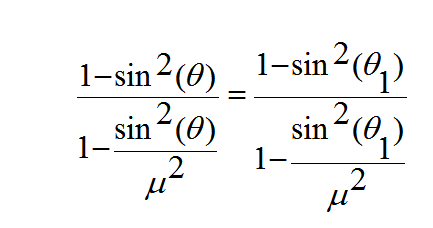(17)
و هذه المعادلة تأخذ الشكل الاتي
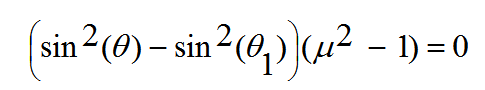(18)
و حيث أن 1 ≠ μ ،فان
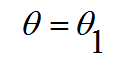(19)
و بالمثل يمكننا استنتاج أن
(20)
أي أنه عند وضع النهاية الصغرى للانحراف زاوية السقوط = زاوية الخروج.
و بالتالي زاوية راس المنشور تأخذ الشكل:
(21)
و المعادلة الاتية:
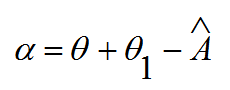
تأخذ الشكل:
و المعادلة (*) يمكن أن تكتب على الصورة:
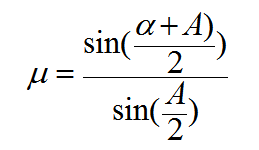(22)
أما إذا كانت زاوية رأس المنشور صغيرة و كانت الأشعة الساقطة على سطح المنشور عمودية تقريبا فان زوايا الانكسار و الانحراف تكون صغيرة كذلك، و من ثم تأخذ المعادلة السابقة الشكل الآتي
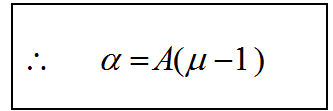(23)
الاكثر قراءة في الضوء
اخر الاخبار
اخبار العتبة العباسية المقدسة
