Now we go on to consider another situation, a very practical one. Most of the lenses that we use have two surfaces, not just one. How does this affect matters? Suppose that we have two surfaces of different curvature, with glass filling the space between them (Fig. 27–5). We want to study the problem of focusing from a point O to an alternate point O′. How can we do that? The answer is this: First, use formula (27.3) for the first surface, forgetting about the second surface. This will tell us that the light which was diverging from O will appear to be converging or diverging, depending on the sign, from some other point, say O′. Now we consider a new problem. We have a different surface, between glass and air, in which rays are converging toward a certain point O′. Where will they actually converge? We use the same formula again! We find that they converge at O′′. Thus, if necessary, we can go through 75 surfaces by just using the same formula in succession, from one to the next!

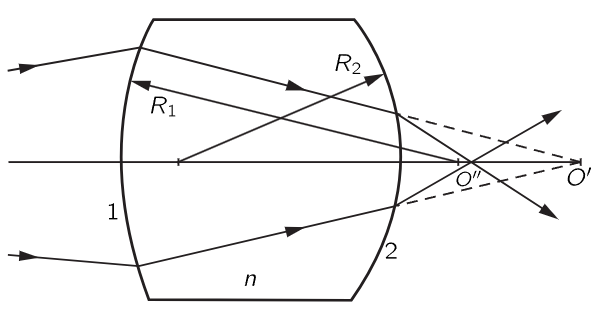
Fig. 27–5. Image formation by a two-surface lens.

There are some rather high-class formulas that would save us considerable energy in the few times in our lives that we might have to chase the light through five surfaces, but it is easier just to chase it through five surfaces when the problem arises than it is to memorize a lot of formulas, because it may be we will never have to chase it through any surfaces at all!

In any case, the principle is that when we go through one surface we find a new position, a new focal point, and then take that point as the starting point for the next surface, and so on. In order to actually do this, since on the second surface we are going from n to 1 rather than from 1 to n, and since in many systems there is more than one kind of glass, so that there are indices n₁, n₂, …, we really need a generalization of formula (27.3) for a case where there are two different indices, n₁ and n₂, rather than only n. Then it is not difficult to prove that the general form of (27.3) is

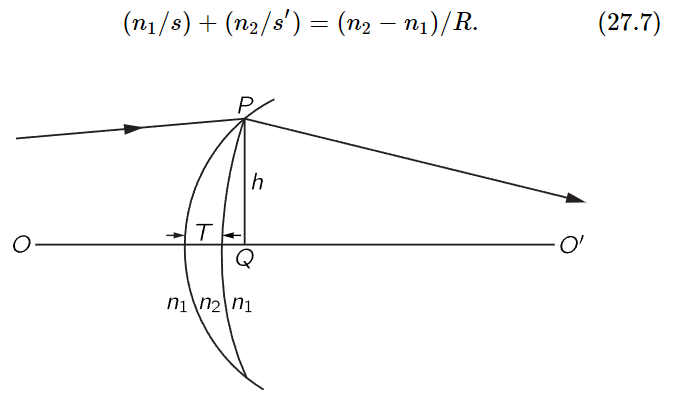
Fig. 27–6. A thin lens with two positive radii.

Particularly simple is the special case in which the two surfaces are very close together—so close that we may ignore small errors due to the thickness. If we draw the lens as shown in Fig. 27–6, we may ask this question: How must the lens be built so as to focus light from O to O′? Suppose the light comes exactly to the edge of the lens, at point P. Then the excess time in going from O to O′ is (n₁h²/2s)+(n₁h²/2s′), ignoring for a moment the presence of the thickness T of glass of index n₂. Now, to make the time for the direct path equal to that for the path OPO′, we have to use a piece of glass whose thickness T at the center is such that the delay introduced in going through this thickness is enough to compensate for the excess time above. Therefore, the thickness of the lens at the center must be given by the relationship

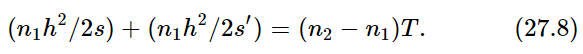
We can also express T in terms of the radii R₁ and R₂ of the two surfaces. Paying attention to our convention (3), we thus find, for R₁<R₂ (a convex lens),

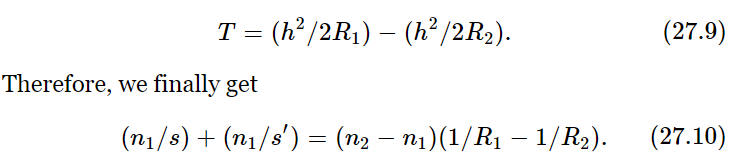
Now we note again that if one of the points is at infinity, the other will be at a point which we will call the focal length f. The focal length f is given by

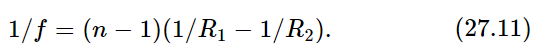
where n=n₂/n₁.

Now, if we take the opposite case, where s goes to infinity, we see that s′ is at the focal length f′. This time the focal lengths are equal. (This is another special case of the general rule that the ratio of the two focal lengths is the ratio of the indices of refraction in the two media in which the rays focus. In this particular optical system, the initial and final indices are the same, so the two focal lengths are equal.)

Forgetting for a moment about the actual formula for the focal length, if we bought a lens that somebody designed with certain radii of curvature and a certain index, we could measure the focal length, say, by seeing where a point at infinity focuses. Once we had the focal length, it would be better to write our equation in terms of the focal length directly, and the formula then is

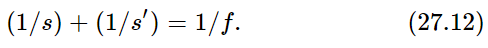
Now let us see how the formula works and what it implies in different circumstances. First, it implies that if s or s′ is infinite the other one is f. That means that parallel light focuses at a distance f, and this in effect defines f. Another interesting thing it says is that both points move in the same direction. If one moves to the right, the other does also. Another thing it says is that s and s′ are equal if they are both equal to 2f. In other words, if we want a symmetrical situation, we find that they will both focus at a distance 2f.